
科目: 来源: 题型:
(1)求f(m)·f(n)的值;
(2)求证:f(x)在区间[m,n]上是增函数;
(3)设f(x)在区间[m,n]上的最大值和最小值分别为M和N,试问当实数a为何值时,M-N取得最小值?并求出这个最小值.
查看答案和解析>>
科目: 来源: 题型:
(1)求证:数列{an+1-an+3}是等比数列;
(2)求数列{an}的通项公式;
(3)求和:Sn=|a1|+|a2|+|a3|+…+|an|(n∈N*).
查看答案和解析>>
科目: 来源: 题型:
(1)求“1号箱子中恰有2个球”发生的概率;
(2)求“每个箱子中至少有1个球”发生的概率;
(3)在(2)发生的情况下,若编号为x号的箱子中有x号球,则称放对了箱子,求“恰好放对了一个箱子”发生的概率.
查看答案和解析>>
科目: 来源: 题型:
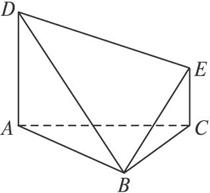
(1)求证:平面ADB⊥平面EDB;
(2)求直线BC与平面EDB所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
(1)求函数f(x)的单调递减区间;
(2)在△ABC中,a、b、c分别是三角形的内角A、B、C所对的边,若f(A)=2,a=![]() ,求b+c的最大值.
,求b+c的最大值.
查看答案和解析>>
科目: 来源: 题型:
①如果PA⊥BC,PB⊥AC,那么点P在平面ABC内的射影是△ABC的垂心;
②如果点P到△ABC的三边所在直线的距离都相等,那么点P在平面ABC内的射影是△ABC的内心;
③如果棱PA和BC所成角为60°,PA=BC=2,E、F分别是棱PB、AC的中点,那么EF=1;
④如果三棱锥P—ABC的各条棱长均为1,则该三棱锥在任意一个平面内的射影的面积都不大于![]() .
.
其中正确命题的序号是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com