
科目: 来源: 题型:
某市对上、下班交通情况做抽样调查,上下班时间各抽取了12辆机动车行驶时速如下(单位km/h):
上班时间:30 33 18 27 32 40 26 28 21 28 35 20
下班时间:27 19 32 29 36 29 30 22 25 16 17 30
用茎叶图表示上面的样本数据,并求出样本数据的中位数.
查看答案和解析>>
科目: 来源: 题型:
已知圆(x+4)2+y2=25的圆心为M1,圆(x-4)2+y2=1的圆心为M2,一动圆与这两个圆都外切.w.w.w.k.s.5.u.c.o.m ![]()
![]()
⑴求动圆圆心P的轨迹方程;
⑵若过点M2的直线与⑴中所求轨迹有两个交点A、B,求|AM1|·|BM1|的取值范围.
查看答案和解析>>
科目: 来源: 题型:
 过圆
过圆![]() 的圆心,作直线分别交x、y正半轴于点A、B,
的圆心,作直线分别交x、y正半轴于点A、B,![]() 被圆分成四部分(如图),若这四部分图形面积满足
被圆分成四部分(如图),若这四部分图形面积满足![]() 则直线AB有( )
则直线AB有( )
(A) 0条 (B) 1条 (C) 2条 (D) 3条
查看答案和解析>>
科目: 来源: 题型:
(本小题满分14分)
某工厂生产一种产品的成本费由三部分组成:
① 职工工资固定支出![]() 元;② 原材料费每件40元;
元;② 原材料费每件40元;
③ 电力与机器保养等费用为每件![]() 元,其中
元,其中![]() 是该厂生产这种产品的总件数.
是该厂生产这种产品的总件数.
(1)把每件产品的成本费![]() (元)表示成产品件数
(元)表示成产品件数![]() 的函数,并求每件产品的最低成本费;
的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量![]() 不超过
不超过![]() 件,且产品能全部销售.根据市场调查:每件产品的销售价
件,且产品能全部销售.根据市场调查:每件产品的销售价![]() 与产品件数
与产品件数![]() 有如下关系:
有如下关系:![]() ,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
查看答案和解析>>
科目: 来源: 题型:
(本小题满分14分)已知关于x的函数f(x)=![]() +bx2+cx+bc,其导函数为f+(x)。令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M。
+bx2+cx+bc,其导函数为f+(x)。令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M。
(Ⅰ)如果函数f(x)在x=1处有极值-![]() ,试确定b、c的值;
,试确定b、c的值;
(Ⅱ)若∣b∣>1,证明对任意的c,都有M>2;
(Ⅲ)若M≥K对任意的b、c恒成立,试求k的最大值。
查看答案和解析>>
科目: 来源: 题型:
把所有正整数按上小下大,左小右大的原则排成如图所示的数表,其中第![]() 行共有
行共有![]() 个正整数.设
个正整数.设![]() (i、j∈N*)表示位于这个数表中从上往下数第i行,从左往右数第j个数.
(i、j∈N*)表示位于这个数表中从上往下数第i行,从左往右数第j个数.
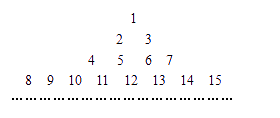
(Ⅰ)若![]() =2010,求i和j的值;
=2010,求i和j的值;
(Ⅱ)记![]()
![]() N*),试比较
N*),试比较![]() 与
与![]()
![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com