
科目: 来源: 题型:
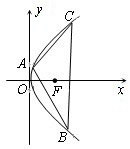
如图,抛物线的顶点在坐标原点,且开口向右,点A,B,C在抛物线上,△ABC的重心F为抛物线的焦点,直线AB的方程为![]() 。
。
(Ⅰ)求抛物线的方程;
(Ⅱ)设点M为某定点,过点M的动直线l与抛物线相交于P,Q两点,试推断是否存在定点M,使得以线段PQ为直径的圆经过坐标原点?若存在,求点M的坐标;若不存在,说明理由。
查看答案和解析>>
科目: 来源: 题型:
设向量![]() 为直角坐标平面内x轴,y轴正方向上的单位向量.若向量
为直角坐标平面内x轴,y轴正方向上的单位向量.若向量![]() ,
,![]()
![]() ,且
,且![]() .
.
(1)求满足上述条件的点![]() 的轨迹方程;
的轨迹方程;
(2)设![]() ,问是否存在常数
,问是否存在常数![]() ,使得
,使得![]() 恒成立?证明你的结论.
恒成立?证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
有一种掷正方体骰子走跳棋的网络游戏,棋盘上标有第0站,第1站,第2站,…,第100站。一枚棋子开始在第0站,玩家每掷一次骰子,棋子向前跳动一次,若掷出朝上的点数为1或2,则棋子向前跳一站;若掷出其余点数,则棋子向前跳两站。游戏规定:若棋子经过若干次跳动恰跳到第99站,则玩家获胜,游戏结束;若棋子经过若干次跳动最后恰跳到第100站,则玩家失败,游戏结束。设棋子跳到第n站的概率为pn (n∈N,n≤100),可以证明:![]() (2≤n≤100),则每次玩该游戏获胜的概率是( )
(2≤n≤100),则每次玩该游戏获胜的概率是( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
我校文化体育艺术节的乒乓球决赛在甲乙两人中进行,比赛规则如下:比赛采用7局4胜制(先胜4局这获胜即比赛结束),在每一局比赛中,先得11分的一方为胜方;比赛没有平局,10平后,先连得2分的一方为胜方。(1)根据以往战况,每局比赛甲胜乙的概率为0.6,设比赛的场数为![]() ,求
,求![]() 的分布列和期望;(2)若双方在每一分的争夺中甲胜的概率也为0.6,求决胜局中甲在以8:9落后的情况下最终以12:10获胜的概率。
的分布列和期望;(2)若双方在每一分的争夺中甲胜的概率也为0.6,求决胜局中甲在以8:9落后的情况下最终以12:10获胜的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com