某校组织一次冬令营活动，有8名同学参加，其中有5名男同学，3名女同学，为了活动的需要，要从这8名同学中随机抽取3名同学去执行一项特殊任务，记其中有X名男同学.

（1）求X的概率分布；

（2）求去执行任务的同学中有男有女的概率.

街道旁边有一游戏：在铺满边长为9 cm的正方形塑料板的宽广地面上，掷一枚半径为1 cm的小圆板，规则如下：每掷一次交5角钱，若小圆板压在正方形的边，可重掷一次；若掷在正方形内，须再交5角钱可玩一次；若掷在或压在塑料板的顶点上，可获1元钱.试问：

（1）小圆板压在塑料板的边上的概率是多少？

（2）小圆板压在塑料板顶点上的概率是多少？

１０.若函数y＝x ³－2x ²＋mx, 当x＝时, 函数取得极大值, 则m的值为  （　　）

A.  3            B.  2           C.  1        D.  

某医院一天派出医生下乡医疗，派出医生人数及其概率如下：

求：（1）派出医生至多2人的概率；

（2）派出医生至少2人的概率.

一个多面体的直观图和三视图（正视图、左视图、俯视图）如图所示，M、N分别为A₁B、B₁C₁的中点.求证：

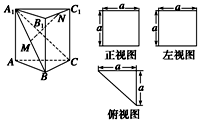
（1）MN∥平面ACC₁A₁；

（2）MN⊥平面A₁BC.

已知ABCD是平行四边形，P点是ABCD所在平面外的一点，连接PA、PB、PC、PD.设点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心.

（1）试用向量方法证明E、F、G、H四点共面；

（2）试判断平面EFGH与平面ABCD的位置关系，并用向量方法证明你的判断.

如图所示，在斜三棱柱A₁B₁C₁—ABC中，底面是等腰三角形，AB=AC，侧面BB₁C₁C⊥底面ABC.

（1）若D是BC的中点.求证：AD⊥CC₁；

（2）过侧面BB₁C₁C的对角线BC₁的平面交侧棱于M，若AM=MA₁，

求证：截面MBC₁⊥侧面BB₁C₁C.

如图所示，等腰直角三角形ABC中，∠A=90°，BC=，DA⊥AC，DA⊥AB，若DA=1，且E为DA的中点.求异面直线BE与CD所成角的余弦值.

对“简单随机抽样”概念的理解错误的是(    )

A.它是一种不放回抽样

B.它是一种有放回抽样

C.它是从总体中逐个进行抽取

D.它要求被抽取样本的总体的个体数有限

三个数成等差数列，如果将最小数乘以2，最大数加上7。所得三数之积为1000，且成等比数列，则原等差数列的公差一定是              （    ）

    A     8                              B       8或 -15

    C                              D