
科目: 来源: 题型:
已知向量![]() (
(![]() cos
cos![]() ,
,![]() sin
sin![]() ) (
) (![]() ≠0 ),
≠0 ),![]() = ( – sin
= ( – sin![]() ,cos
,cos![]() ),其中O为坐标原点。(1)若
),其中O为坐标原点。(1)若![]() =
=![]() –
– ![]() ,求向量
,求向量![]() 与
与![]() 的夹角;(2)若|
的夹角;(2)若|![]() |≥2|
|≥2|![]() |对任意实数
|对任意实数![]() 、
、![]() 都成立,求实数
都成立,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目: 来源: 题型:
数列![]() 的各项均为正数,
的各项均为正数,![]() 为其前
为其前![]() 项和,对于任意
项和,对于任意![]() ,总有
,总有![]() 成等差数列.
成等差数列.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若b![]() =a
=a![]() 4
4![]() (
(![]() ), B
), B![]() 是数列{b
是数列{b![]() }的前
}的前![]() 项和, 求证:不等式 B
项和, 求证:不等式 B![]() ≤4B
≤4B![]() ,对任意
,对任意![]() 皆成立.
皆成立.
(3)令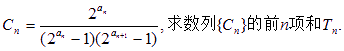
查看答案和解析>>
科目: 来源: 题型:
 (本题满分14分)已知如图,椭圆方程为
(本题满分14分)已知如图,椭圆方程为![]()
![]() .P为椭圆上的动点,
.P为椭圆上的动点,
F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角
平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.
(1)求M点的轨迹T的方程;(2)已知![]() 、
、![]() ,
,
试探究是否存在这样的点![]() :
:![]() 是轨迹T内部的整点
是轨迹T内部的整点
(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积![]() ?
?
若存在,求出点Q的坐标,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
某公司按现有能力,每月收入为70万元,公司分析部门测算,若不进行改革,入世后因竞争加剧收入将逐月减少.分析测算得入世第一个月收入将减少3万元,以后逐月多减少2万元,如果进行改革,即投入技术改造300万元,且入世后每月再投入1万元进行员工培训,则测算得自入世后第一个月起累计收入![]() 与时间n(以月为单位)的关系为
与时间n(以月为单位)的关系为![]() =
=![]() ,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.
,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.
查看答案和解析>>
科目: 来源: 题型:
(本题14分)一个袋中装有大小相同的黑球、白球和红球,已知袋中共有10个球,从中任意摸出1个球,得到黑球的概率是![]() ;从中任意摸出2个球,至少得到1个白球的概率是
;从中任意摸出2个球,至少得到1个白球的概率是![]() 。求:
。求:
(Ⅰ)从中任意摸出2个球,得到的数是黑球的概率;
(Ⅱ)袋中白球的个数。
查看答案和解析>>
科目: 来源: 题型:
若f (x)是定义在R上的偶函数,其图象关于直线x=2对称,且当x∈(-2, 2) 时,f (x) =-x2+1. 则当x∈(-6,-2)时,f(x)=_______ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com