一袋中有m(m∈N^*)个红球，3个黑球和2个自球，现从中任取2个球．

   （Ⅰ）当m=4时，求取出的2个球颜色相同的概率；

   （Ⅱ）当m=3时，设ξ表示取出的2个球中黑球的个数，求ξ的概率分布及数学期望；

   （Ⅲ）如果取出的2个球颜色不相同的概率小于，求m的最小值．

已知甲、乙两名射击运动员各自独立地射击1次，命中10环的概率分别为、x(x＞)；且运动员乙在两次独立射击中恰有1次命中10环的概率为．

（Ⅰ）求的值；

（Ⅱ）若甲、乙两名运动员各自独立地射击1次，设两人命中10环的次数之和为随机变量，求的分布列及数学期望．

已知函数 .

（Ⅰ）若在上是增函数, 求实数a的取值范围.

（Ⅱ）若是的极大值点,求在上的最大值；

（Ⅲ）在（2）的条件下，是否存在实数b，使得函数的图像与函数的图像恰有3个交点，若存在，求出b的取值范围，若不存在，说明理由.

已知△的面积等于最大边，，则    ．

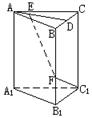
如图：已知直三棱柱ABC—A₁B₁C₁，AB＝AC，F为棱BB₁上一点，BF∶FB₁＝2∶1，BF＝BC＝2a。

　　（I）若D为BC的中点，E为AD上不同于A、D的任意一点，证明EF⊥FC₁；

　　（II）试问：若AB＝2a，在线段AD上的E点能否使EF与平面BB₁C₁C成60°角，为什么？证明你的结论

如图，在边长为的正方形中，点是的中点，点是的中点，将△AED,△DCF分别沿折起，使两点重合于.

（1） 求证:；

（2） 求二面角的正切值.

已知函数

   （1）求

   （2）当的值域。

设函数定义域为，当时,,且对于任意的,都有 

（1）求的值,并证明函数在上是减函数；

（2）记△ABC的三内角A、B、C的对应边分别为a，b，c，若时，不等式恒成立，求实数的取值范围。

在等比数列中，，公比，前项和，求首项和项数

的展开式中的系数为          .