
科目: 来源: 题型:
某商场在七月初七举行抽奖促销活动,要求一男一女参加抽奖,抽奖规则是:从装有3个白球和2个红球的箱子中每次随机地摸出一个球,记下颜色后放回. 若1人摸出一个红球得奖金10元,1人摸出2个红球得奖金50元. 规定:一对男女中男的摸一次,女的摸二次.令![]() 表示两人所得奖金总额.
表示两人所得奖金总额.
(1)求![]() =20时的概率;
=20时的概率;
(2)求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目: 来源: 题型:
一个不透明的口袋内装有材质、重量、大小相同的7个小球,且每个小球的球面上要么只写有数字“08”,要么只写有文字“奥运”.假定每个小球每一次被取出的机会都相同,又知从中摸出2个球都写着“奥运”的概率是![]() 。现甲、乙两个小朋友做游戏,方法是:不放回从口袋中轮流摸取一个球,甲先取、乙后取,然后甲再取,直到两个小朋友中有1人取得写着文字“奥运”的球时游戏终止,每个球在每一次被取出的机会均相同.
。现甲、乙两个小朋友做游戏,方法是:不放回从口袋中轮流摸取一个球,甲先取、乙后取,然后甲再取,直到两个小朋友中有1人取得写着文字“奥运”的球时游戏终止,每个球在每一次被取出的机会均相同.
(1)求该口袋内装有写着数字“08”的球的个数;
(2)求当游戏终止时总球次数不多于3的概率.
查看答案和解析>>
科目: 来源: 题型:
对任意![]() ,给定区间
,给定区间![]() ,设函数
,设函数![]() 表示实数
表示实数![]() 与
与![]() 的给定区间内整数之差的绝对值.
的给定区间内整数之差的绝对值.
|
(2)判断函数![]()
![]() R)的奇偶性,并证明你的结论;
R)的奇偶性,并证明你的结论;
(3)求方程![]() 的实根.(要求说明理由)
的实根.(要求说明理由)
查看答案和解析>>
科目: 来源: 题型:
如图,在底面是直角梯形的四棱锥![]() 中,AD∥BC,∠ABC=90°,且
中,AD∥BC,∠ABC=90°,且![]() ,又PA⊥平面ABCD,AD=3AB=3PA=3a。
,又PA⊥平面ABCD,AD=3AB=3PA=3a。
(I)求二面角P—CD—A的正切值;
(II)求点A到平面PBC的距离。

查看答案和解析>>
科目: 来源: 题型:
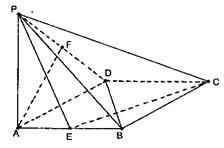
如图,已知:在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=AB=2,E,F分别是AB与PD的中点.
(1)求证:PC⊥BD;
(2)求证:AF//平面PEC;
(3)求二面角P—EC—D的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com