设P是一个数集，且至少含有两个数，若对任意a、b∈R，都有a+b、a-b， ab、　∈P（除数b≠0），则称P是一个数域.例如有理数集Q是数域；数集也是数域.有下列命题：

①整数集是数域；                     ②若有理数集，则数集M必为数域；

③数域必为无限集；                  ④存在无穷多个数域。

其中正确的命题的序号是          。（把你认为正确的命题的序号填填上）

已知全集U，A，B，那么         ___.

（本小题满分12分）

某柑桔基地因冰雪灾害，使得果林严重受损，为此有关专家提出两种拯救果林的方案，每种方案都需分两年实施；若实施方案一，预计当年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4；第二年可以使柑桔产量为上一年产量的1.25倍、1.0倍的概率分别是0.5、0.5. 若实施方案二，预计当年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5； 第二年可以使柑桔产量为上一年产量的1.2倍、1.0倍的概率分别是0.4、0.6. 实施每种方案，第二年与第一年相互独立。令表示方案实施两年后柑桔产量达到灾前产量的倍数。

（1）写出的分布列；

（2）实施哪种方案，两年后柑桔产量超过灾前产量的概率更大？

（3）不管哪种方案，如果实施两年后柑桔产量达不到灾前产量，预计可带来效益10万元；两年后柑桔产量恰好达到灾前产量，预计可带来效益15万元；柑桔产量超过灾前产量，预计可带来效益20万元；问实施哪种方案所带来的平均效益更大？

（本小题满分13分）

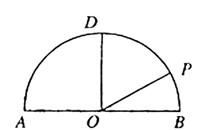
如图，在以点O为圆心，|AB|=4为直径的半圆ADB中，OD⊥AB，P是半圆弧上一点，

∠POB=30°，曲线C是满足||MA|-|MB||为定值的动点M的轨迹，且曲线C过点P。

（Ⅰ）建立适当的平面直角坐标系，求曲线C的方程；

（Ⅱ）设过点D的直线l与曲线C相交于不同的两点E、F。若△OEF的面积不小于2，求直线l斜率的取值范围。

.(本小题满分12分)

水库的蓄水量随时间而变化，现用t表示时间，以月为单位，年初为起点，根据历年数据，某水库的蓄水量（单位：亿立方米）关于t的近似函数关系式为

V（t）=。

（Ⅰ）该水库的蓄求量小于50的时期称为枯水期，以i-1＜t＜t表示第1月份（i=1,2,…,12），同一年内哪几个月份是枯水期？

（Ⅱ）求一年内该水库的最大蓄水量（取e=2.7计算）

(3’+5’+8’)设P(a,b)（b≠0）是平面直角坐标系xOy中的点，l是经过原点与点(1,b)的直线，记Q是直线l与抛物线x²＝2py（p≠0）的异于原点的交点

（1）若a＝1，b＝2，p＝2，求点Q的坐标；

（2）若点P(a,b)（ab≠0）在椭圆+y²＝1上，p＝，

求证：点Q落在双曲线4x²－4y²＝1上；

（3）若动点P(a,b)满足ab≠0，p＝，若点Q始终落在一条关于x轴对称的抛物线上，试问动点P的轨迹落在哪种二次曲线上，并说明理由.

（）（本小题满分12分）

如图，已知点P在正方体ABCD-的对角线上，。

（Ⅰ）求DP与所成角的大小；

（Ⅱ）求DP与平面所成角的大小。

若不等式的解集为A，且，求a的取值范围。

设，若函数有大于零的极值点，则

       A．   B．    C．   D．

已知复数均为实数，为虚数单位，且对于任意复数。

（1）试求的值，并分别写出和用、表示的关系式；

（2）将(、)作为点的坐标，(、)作为点的坐标，上述关系可以看作是坐标平面上点的一个变换：它将平面上的点变到这一平面上的点，

当点在直线上移动时，试求点经该变换后得到的点的轨迹方程；

（3）是否存在这样的直线：它上面的任一点经上述变换后得到的点仍在该直线上？若存在，试求出所有这些直线；若不存在，则说明理由。