
科目: 来源: 题型:
(本小题满分12分)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AB//CD,AB⊥AD,AD=CD=2AB=2.侧面![]() 为正三角形,且平面PAD⊥平面ABCD.
为正三角形,且平面PAD⊥平面ABCD.
(1)若M为PC上一动点,则M在何位置时,PC⊥平面MDB?并加已证明.
(2)若G为![]() 的重心,求二面角G—BD—C大小。
的重心,求二面角G—BD—C大小。
查看答案和解析>>
科目: 来源: 题型:
()从5名男医生、4名女医生中选3名医生组成一个医疗小分队,要求其中男、女医生都有,则不同的组队方案共有
(A)70种 (B) 80种 (C) 100种 (D)140种
查看答案和解析>>
科目: 来源: 题型:
对于四面体ABCD,下列命题正确的是 (写出所有正确命题的编号)。
①相对棱AB与CD所在的直线异面;
②由顶点A作四面体的高,其垂足是![]() BCD的三条高线的交点;
BCD的三条高线的交点;
③若分别作![]() ABC和
ABC和![]() ABD的边AB上的高,则这两条高所在直线异面;
ABD的边AB上的高,则这两条高所在直线异面;
④分别作三组相对棱中点的连线,所得的三条线段相交于一点;
⑤最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱。
查看答案和解析>>
科目: 来源: 题型:
已知函数![]()
![]() ,函数
,函数![]() 的图像与函数
的图像与函数![]()
![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,
,
求实数![]() 的取值范围;
的取值范围;
(3)设函数![]()
![]() ,试用列举法表示集合
,试用列举法表示集合![]() .
.
查看答案和解析>>
科目: 来源: 题型:
如图所示,在直角梯形ABCP中,AB=BC=3,AP=7,CD⊥AP,现将![]() 沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
(I)求证:PA//平面EFG;
(II)若M为线段CD上的一个动点,问当M在什么位置时,MF与平面EFG所成角最大。
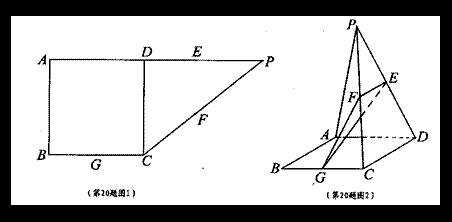
查看答案和解析>>
科目: 来源: 题型:
设函数![]() .
.
(1)若![]() 时函数
时函数![]() 有三个互不相同的零点,求
有三个互不相同的零点,求![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 内没有极值点,求
内没有极值点,求![]() 的取值范围;
的取值范围;
(3)若对任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
已知函数![]() ,且
,且![]() 。
。
(I)试用含![]() 的代数式表示
的代数式表示![]() ;
;
(Ⅱ)求![]() 的单调区间;
的单调区间;
(Ⅲ)令![]() ,设函数
,设函数![]() 在
在![]() 处取得极值,记点
处取得极值,记点![]() ,证明:线段
,证明:线段![]() 与曲线
与曲线![]() 存在异于
存在异于![]() 、
、![]() 的公共点。
的公共点。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com