
科目: 来源: 题型:
如图3,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点。
(1)求证:EF//平面PAD;
(2)求证:EF⊥CD;
(3)若∠PDA=450,求EF与平面ABCD所成的角的大小
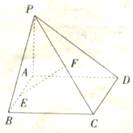
查看答案和解析>>
科目: 来源: 题型:
某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床每天的租金)不超过10元时,床位可以全部租出,当床位高于10元时,每提高1元,将有3张床位空闲.为了获得较好的效益,该宾馆要给床位一个合适的价格,条件是:①要方便结帐,床价应为1元的整数倍;② 该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高出得越多越好.若用![]() 表示床价,用
表示床价,用![]() 表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)
表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)
(1)把![]() 表示成
表示成![]() 的函数,并求出其定义域;
的函数,并求出其定义域;
(2)试确定该宾馆将床位定价为多少时既符合上面的两个条件,又能使净收入最多?
查看答案和解析>>
科目: 来源: 题型:
(12分)设数列{an},{bn}都是等差数列,它们的前n项的和分别为Sn , Tn ,若对一切n ∈ N*,都有Sn+3 = Tn .(1)若a1 ≠ b1,试分别写出一个符号条件的数列{an}和{bn};(2)若a1 + b1 = 1,数列{cn}满足:cn = 4 an + l(–1)n–12 bn,且当n ∈ N*时,cn+1 ≥ cn恒成立,求实数l的最大值.
查看答案和解析>>
科目: 来源: 题型:
已知某同学上学途中必须经过三个交通岗,且在每一个交通岗遇到红灯的概率均为![]() ,假设他在3个交通岗遇到红灯的事件是相互独立的,用随机变量
,假设他在3个交通岗遇到红灯的事件是相互独立的,用随机变量![]() 表示该同学遇到红灯的次数.
表示该同学遇到红灯的次数.
(1)求该同学在第一个交通岗遇到红灯,其它交通岗未遇到红灯的概率;
(2)若![]() ,则该同学就迟到,求该同学不迟到的概率;
,则该同学就迟到,求该同学不迟到的概率;
(3)求随机变量![]() 的数学期望和方差
的数学期望和方差
查看答案和解析>>
科目: 来源: 题型:
(本题满分12分) 直角三角形![]() 的直角顶点
的直角顶点![]() 为动点,
为动点,![]() ,
,![]() 为两个定点,作
为两个定点,作![]() 于
于![]() ,动点
,动点![]() 满足
满足![]() ,当点
,当点![]() 运动时,设点
运动时,设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,曲线
,曲线![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() .(Ⅰ) 求曲线
.(Ⅰ) 求曲线![]() 的方程;(Ⅱ) 是否存在方向向量为m
的方程;(Ⅱ) 是否存在方向向量为m![]() 的直线
的直线![]() ,与曲线
,与曲线![]() 交于
交于![]() ,
,![]() 两点,使
两点,使![]() ,且
,且![]() 与
与![]() 的夹角为
的夹角为![]() ?若存在,求出所有满足条件的直线方程;若不存在,说明理由.
?若存在,求出所有满足条件的直线方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com