某公司有价值万元的一条流水线，要提高该流水线的生产能力，就要对其进行技术改造，从而提高产品附加值，改造需要投入，假设附加值万元与技术改造投入万元之间的关系满足：①与和的乘积成正比；②时，；③，其中为常数，且。

（1）设，求表达式，并求的定义域；

（2）求出附加值的最大值，并求出此时的技术改造投入。

某市旅游部门开发一种旅游纪念品，每件产品的成本是元，销售价是元，月平均销售件.通过改进工艺，产品的成本不变，质量和技术含金量提高，市场分析的结果表明，如果产品的销售价提高的百分率为，那么月平均销售量减少的百分率为.记改进工艺后，旅游部门销售该纪念品的月平均利润是（元）.

(Ⅰ)写出与的函数关系式；

(Ⅱ)改进工艺后，确定该纪念品的售价，使旅游部门销售该纪念品的月平均利润最大.

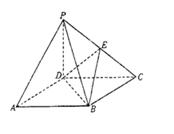
如图，四棱锥P—ABCD的底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点.

   （1）证明PA//平面BDE；    

   （2）求二面角B—DE—C的平面角的余弦值；

   （3）在棱PB上是否存在点F，使PB⊥平面DEF？证明你的结论.

如图，四棱锥P—ABCD中，底面四边形ABCD是正方形，侧面PDC是边长为a的正

三角形，且平面PDC⊥底面ABCD，E为PC的中点。

         （II）求点D到面PAB的距离.

如图，已知点H在正方体的对角线上，∠HDA=．

（Ⅰ）求DH与所成角的大小；

（Ⅱ）求DH与平面所成角的大小．

（本小题满分12分） 在等差数列中，，数列满足，且（1）求数列的通项公式；    （2）求数列的前项的和.

在公差为的等差数列中,成等比数列,则

    A．          B．            C．           D．

已知集合P=[，2]，函数y= log₂(ax²-2x+2)的定义域为Q。

（1）若PQ，求实数a的取值范围；

（2）若方程log₂(ax²-2x+2)=2在[，2]内有解，求实数a的取值范围。

袋子里有大小相同的3个红球和4个黑球，今从袋子里随机取球.

　　（Ⅰ）若有放回地摸出4个球，求取出的红球数不小于黑球数的概率；

　　（Ⅱ）若无放回地摸出4个球，

①求取出的红球数ξ的概率分布列和数学期望；

②求取出的红球数不小于黑球数的概率，并比较的大小.

要完成下列两项调查：①从某社区125户高收入家庭，280户中等收入家庭，95户低收入家庭中选出100户调查社会购买力的某项指标；②从某中学高一年级的12名体育特长生中选出3人调查学习负担情况。应采用的抽样方法是

       A．①用随机抽样法，②用系统抽样法

       B．①用分层抽样法，②用随机抽样法

       C．①用系统抽样法，②用分层抽样法

       D．①、②都用分层抽样法