
科目: 来源: 题型:
某工厂生产甲、乙两种产品,甲产品的一等品率为80%,二等品率为20%;乙产品的一等品率为90%,二等品率为10%。生产1件甲产品,若是一等品则获得利润4万元,若是二等品则亏损1万元;生产1件乙产品,若是一等品则获得利润6万元,若是二等品则亏损2万元。设生产各种产品相互独立。
(1)记X(单位:万元)为生产1件甲产品和1件乙产品可获得的总利润,求X的分布列;
(2)求生产4件甲产品所获得的利润不少于10万元的概率。
查看答案和解析>>
科目: 来源: 题型:
设![]() 是定义在区间
是定义在区间![]() 上的函数,其导函数为
上的函数,其导函数为![]() 。如果存在实数
。如果存在实数![]() 和函数
和函数![]() ,其中
,其中![]() 对任意的
对任意的![]() 都有
都有![]() >0,使得
>0,使得![]() ,则称函数
,则称函数![]() 具有性质
具有性质![]() 。
。
(1)设函数![]()
![]() ,其中
,其中![]() 为实数。
为实数。
(i)求证:函数![]() 具有性质
具有性质![]() ; (ii)求函数
; (ii)求函数![]() 的单调区间。
的单调区间。
(2)已知函数![]() 具有性质
具有性质![]() 。给定
。给定![]() 设
设![]() 为实数,
为实数,
![]() ,
,![]() ,且
,且![]() ,
,
若|![]() |<|
|<|![]() |,求
|,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目: 来源: 题型:
设各项均为正数的数列![]() 的前n项和为
的前n项和为![]() ,已知
,已知![]() ,数列
,数列![]() 是公差为
是公差为![]() 的等差数列。
的等差数列。
(1)求数列![]() 的通项公式(用
的通项公式(用![]() 表示);
表示);
(2)设![]() 为实数,对满足
为实数,对满足![]() 的任意正整数
的任意正整数![]() ,不等式
,不等式![]() 都成立。求证:
都成立。求证:![]() 的最大值为
的最大值为![]() 。
。
查看答案和解析>>
科目: 来源: 题型:
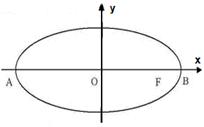
在平面直角坐标系![]() 中,如图,已知椭圆
中,如图,已知椭圆![]() 的左、右顶点为A、B,右焦点为F。设过点T(
的左、右顶点为A、B,右焦点为F。设过点T(![]() )的直线TA、TB与椭圆分别交于点M
)的直线TA、TB与椭圆分别交于点M![]() 、
、![]() ,其中m>0,
,其中m>0,![]() 。
。
(1)设动点P满足![]() ,求点P的轨迹;
,求点P的轨迹;
(2)设![]() ,求点T的坐标;
,求点T的坐标;
(3)设![]() ,求证:直线MN必过x轴上的一定点(其坐标与m无关)。
,求证:直线MN必过x轴上的一定点(其坐标与m无关)。
查看答案和解析>>
科目: 来源: 题型:
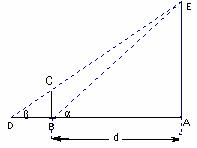
某兴趣小组测量电视塔AE的高度H(单位:m),如示意图,垂直放置的标杆BC的高度h=4m,仰角∠ABE=![]() ,∠ADE=
,∠ADE=![]() 。
。
(1)该小组已经测得一组![]() 、
、![]() 的值,tan
的值,tan![]() =1.24,tan
=1.24,tan![]() =1.20,请据此算出H的值;
=1.20,请据此算出H的值;
(2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使![]() 与
与![]() 之差较大,可以提高测量精确度。若电视塔的实际高度为125m,试问d为多少时,
之差较大,可以提高测量精确度。若电视塔的实际高度为125m,试问d为多少时,![]() -
-![]() 最大?
最大?
查看答案和解析>>
科目: 来源: 题型:
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900。
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离。
查看答案和解析>>
科目: 来源: 题型:
在平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C(-2,-1)。
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长;
(2)设实数t满足(![]() )·
)·![]() =0,求t的值。
=0,求t的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com