
科目: 来源: 题型:
一个三角形数表按如下方式构成:第一行依次写上n(n≥4)个数,在上一行的每相邻两数的中间正下方写上这两数之和,得到下一行,依此类推.记数表中第i行的第j个数为f(i,j).
(1)若数表中第i (1≤i≤n-3)行的数依次成等差数列,求证:第i+1行的数也依次成等差数列;
(2)已知f(1,j)=4j,求f(i,1)关于i的表达式;
(3)在(2)的条件下,若f(i,1)=(i+1)(ai-1),bi= ![]() ,试求一个函数g(x),使得
,试求一个函数g(x),使得
Sn=b1g(1)+b2g(2)+…+bng(n)<![]() ,且对于任意的m∈(
,且对于任意的m∈(![]() ,
,![]() ),均存在实数l ,使得当n>l时,都有Sn >m.
),均存在实数l ,使得当n>l时,都有Sn >m.
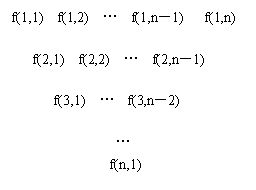
查看答案和解析>>
科目: 来源: 题型:
已知数列![]() 的首项
的首项![]() ,
,![]() .
.
(1)求证:数列 为等比数列;
为等比数列;
(2) 记![]() ,若
,若![]() ,求最大的正整数
,求最大的正整数![]() .
.
(3)是否存在互不相等的正整数![]() ,使
,使![]() 成等差数列且
成等差数列且![]() 成等比数列,如果存在,请给出证明;如果不存在,请说明理由.
成等比数列,如果存在,请给出证明;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
某公司计划2011年在甲、乙两个电视台做总时间不超过300分钟的广告,广告费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟.假定甲、乙两个电视台为该公司每分钟所做的广告,能给公司带来的收益分别为0.3 万元和0.2万元.问:该公司如何分配在甲、乙两个电视台的广告时间,才能使公司收益最大,最大收益是多少万元?
查看答案和解析>>
科目: 来源: 题型:
数列![]() 的前n项和为
的前n项和为![]() ,点
,点![]() 均在函数y=-x+9的图像上.
均在函数y=-x+9的图像上.
(1)求数列![]() 的通项公式和数列
的通项公式和数列![]() 的前n项的和.
的前n项的和.
(2)设![]() , 求数列
, 求数列![]() 的前
的前![]() 项和
项和![]()
(3)设![]()
![]() (
(![]() ),是否存在最大整数
),是否存在最大整数![]() ,使得对任意的
,使得对任意的![]() ,均有
,均有![]() 成立,若存在,求出
成立,若存在,求出![]() 值;若不存在,请说明理由。
值;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
有以下四个命题: ①对于任意实数![]() ,
,![]() ;
;
②设![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,若
项和,若![]() 为一个确定的常数,则
为一个确定的常数,则![]() 也是一个确定的常数;
也是一个确定的常数;
③关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,则关于
,则关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ;
;
④对于任意实数![]() ,
,![]() .
.
其中正确命题的是_______________(把正确的答案题号填在横线上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com