
科目: 来源: 题型:
已知椭圆C的左、右焦点坐标分别是![]() ,
,![]() ,离心率是
,离心率是![]() ,直线y=t与 椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P。
,直线y=t与 椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P。
(Ⅰ)求椭圆C的方程;
(Ⅱ)若圆P与x轴相切,求圆心P的坐标;
(Ⅲ)设Q(x,y)是圆P上的动点,当t变化时,求y的最大值。
查看答案和解析>>
科目: 来源: 题型:
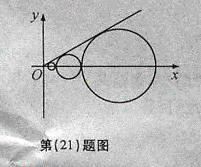
设![]() 是坐标平面上的一列圆,它们的圆心都在
是坐标平面上的一列圆,它们的圆心都在![]() 轴的正半轴上,且都与直线
轴的正半轴上,且都与直线![]() 相切,对每一个正整数
相切,对每一个正整数![]() ,圆
,圆![]() 都与圆
都与圆![]() 相互外切,以
相互外切,以![]() 表示
表示![]() 的半径,已知
的半径,已知![]() 为递增数列.
为递增数列.
(Ⅰ)证明:![]() 为等比数列;
为等比数列;
(Ⅱ)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和.
项和.
 |
查看答案和解析>>
科目: 来源: 题型:
已知实数a满足1<a≤2,设函数f (x)=![]() x3-
x3-![]() x2+ax.
x2+ax.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=4x3+3bx2-6(b+2)x (b∈R) 的极小值点与f (x)的极小值点相同,
求证:g(x)的极大值小于等于10.
查看答案和解析>>
科目: 来源: 题型:
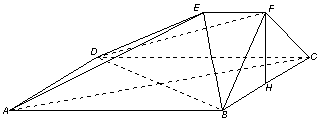
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,
(Ⅰ)求证:FH∥平面EDB;
(Ⅱ)求证:AC⊥平面EDB;
(Ⅲ)求四面体B—DEF的体积;
 |
查看答案和解析>>
科目: 来源: 题型:
已知定义在R上的函数y=f(x)满足以下三个条件:
(1)对任意的x∈R,都有f(x+4)=f(x);
(2)对任意的x1,x2∈R,且0≤x1<x2≤2,都有f(x1)<f(x2);
(3)函数y=f(x+2)的图像关于y轴对称.
则a=f(4.5),b=f(6.5),c=f(7)从小到大的关系是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com