(I)求函数的单调区间；

  (Ⅱ)函数在区间[1，2]上是否有零点，若有，求出零点，若没有，请说明理由；

  (Ⅲ)若任意的∈(1，2)且≠，证明：(注：

 已知焦点在轴上的椭圆C₁：=1经过A(1，0)点，且离心率为．

  (I)求椭圆C₁的方程；

  (Ⅱ)过抛物线C₂：(h∈R)上P点的切线与椭圆C₁交于两点M、N，记线段MN与PA的中点分别为G、H，当GH与轴平行时，求h的最小值．

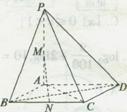
 如图，在四棱锥P—ABCD中，底面ABCD是正方形，PA⊥底面ABCD，且PA=AB，M、N

    分别是PA、BC的中点．

(I)求证：MN∥平面PCD；

(II)在棱PC上是否存在点E，使得AE上平面PBD?若存在，求出AE与平面PBC所成角的正弦值，若不存在，请说明理由．

某工科院校对A,B两个专业的男女生人数进行调查，得到如下的列联表：

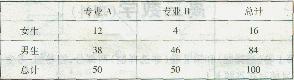
(I)能否在犯错误的概率不超过0．05的前提下，认为工科院校中“性别”与“专业”有关系呢?

(II)从专业A中随机抽取2名学生，记其中女生的人数为X，求X的分布列和均值．

注：

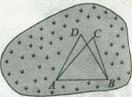
某城市有一块不规则的绿地如图所示，城建部门欲在该地上建造一个底座为三角形的环境标志，小李、小王设计的底座形状分别为△ABC、△ABD，经测量AD=BD=14，BC=10,AC=16,∠C=∠D．

(I)求AB的长度；

(Ⅱ)若建造环境标志的费用与用地面积成正比，不考虑其他因素，小李、小王谁的设计使建造费用最低，请说明理由．

已知等差数列{},为其前n项的和，=6，=18，n∈N^*．

    (I)求数列{}的通项公式；

    (II)若=3，求数列{}的前n项的和．

曲线Ｃ：与轴的交点关于原点的对称点称为“望点”，以“望点”为圆心，凡是与曲线C有公共点的圆，皆称之为“望圆”，则当a=1，b=1时，所有的“望圆”中，面积最小的“望圆”的面积为    ．

△ABC中，∠C=90°，且CA=CB=3，点M满足2，则·=    ．

经调查某地若干户家庭的年收入 (万元)和年饮食支出(万元)具有线性相关关系，并得到关于的线性回归直线方程：=0．254+0．321，由回归直线方程可知，家庭年收入每增加l万元，年饮食支出平均增加    万元．

已知焦点在轴上的双曲线的渐近线方程是，则该双曲线的离心率为（    ）．