选修4-4：坐标系与参数方程

在平面直角坐标系xoy中，已知曲线C₁：x²+y²=1，以平面直角坐标系xoy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线l：ρ(2cosθ-sinθ)=6.

（Ⅰ）将曲线C₁上的所有点的横坐标，纵坐标分别伸长为原来的、2倍后得到曲线C₂，试写出直线l的直角坐标方程和曲线C₂的参数方程.

（Ⅱ）在曲线C₂上求一点P，使点P到直线l的距离最大，并求出此最大值．

选修4-1：几何证明选讲

如图，直线经过⊙上的点，并且⊙交直线于，，连接．

（I）求证：直线是⊙的切线；

（II）若⊙的半径为，求的长．

设，   ．

（1）当时，求曲线在处的切线方程；

（2）如果存在，使得成立，求满足上述条件的最大整数；

（3）如果对任意的，都有成立，求实数的取值范围．

已知椭圆C：=1（a>b>0）的离心率为，以原点为圆点，椭圆的短半轴为半径的圆与直线x-y+=0相切。

（Ⅰ）求椭圆的标准方程；

（Ⅱ）设P（4，0），A,B是椭圆C上关于x轴对称的任意两个不同的点，连接PB交随圆C于另一点E，证明直线AE与x轴相交于定点Q；

学校游园活动有这样一个游戏项目：甲箱子里装有3个白球，2个黑球，乙箱子里装有1个白球，2个黑球，这些球除颜色外完全相同。每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖(每次游戏结束后将球放回原箱)

(1)求在一次游戏中

①摸出3个白球的概率；②获奖的概率。

(2)求在两次游戏中获奖次数X的分布列及数学期望E(x)。

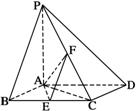
如图，已知四棱锥P-ABCD,底面ABCD为蓌形，PA⊥平面ABCD,∠ABC=60°，E,F分别是BC,PC的中点。 

（Ⅰ）求证：AE⊥PD；

（Ⅱ）若直线PB与平面PAD所成角的正弦值为，求二面角E-AF-C的余弦值．

设数列{}的前n项和满足:＝n－2n（n－1）．等比数列{}的前n项和为，公比为，且＝＋2．

 （1）求数列{}的通项公式；

 （2）设数列{}的前n项和为，求证：≤<．

关于有以下命题：

①若则；  ②图象与图象相同；

③在区间上是减函数；  ④图象关于点对称。

其中正确的命题是            。

已知曲线在点（）处的切线斜率为-2，且是的极值点，则a-b=        .

正四面体ABCD的外接球的球心为0,E是BC的中点，则直线OE与平面BCD所成角的正切值为 　　　　　　 .