已知一个平面，为空间中的任意一条直线，那么在平面内一定存在直线b使得（  ）

       A、//b                  B、与b相交          C、与b是异面直线  D、⊥b

命题“”是命题“”的（   ）

       A、充分不必要条件    B、必要不充分条件 

       C、充要条件            D、既不是充分又不是必要条件

记全集则图中阴影部分所表示的集合是（   ）

       A、           B、                   C、           D、

选修4—5，不等式选讲

已知函数   

（I）若不等式的解集为，求实数的值。

（II）在（I）条件下，若存在实数使成立，求实数m的取值范围。

选修4—4：坐标系与参数方程

在直角坐标系中，圆C的参数方程为                  （为参数）

以O为极点，轴的非负半轴为极轴，并取相同的长度单位建立极坐标系，直线的极坐标方程

（I）求圆心的极坐标。

（II）若圆C上点到直线的最大距离为3，求的值。

选修4—1：几何证明选讲

如图设M为线段AB中点，AE与BD交于点C  ∠DME=∠A=∠B=，且DM交AC于F，EM交BD于G。

（I）写出图中三对相似三角形，并对其中一对作出证明。

（II）连结FG，设=45°，AB=4，AF=3，求FG长

已知函数 ，为的导数。

（I）当=－3时证明在区间（－1，1）上不是单调函数。

（II）设，是否存在实数，对于任意的存在，使得成立？若存在求出的取值范围；若不存在说明理由。

设椭圆的一个顶点A（0，－1），焦点在轴上，若右焦点到直线=0距离为3。

（I）求椭圆的标准方程。

（II）设椭圆与直线相交于不同的两点M、N，当时，求的取值范围。

如图三棱柱ABC－A₁B₁C₁中,每个侧面都是正方形,D为底边AB中点,E为侧棱CC₁中点,AB₁与A₁B交于点O。

（I）求证：CD//平面A₁EB。    

（II）求证：平面AB₁C⊥平面A₁EB

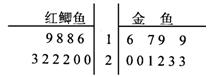
某观赏鱼池塘中养殖大量的红鲫鱼与金鱼，为了估计池中两种鱼数量情况，养殖人员从池中捕出红鲫鱼和金鱼各1000只，并给每只鱼作上不影响其存活的记号，然后放回池内，经过一定时间后，再从池中随机捕出1000只鱼，分别记录下其中有记号的鱼数目，再放回池中，这样的记录作了10次，将记录数据制成如右的茎叶图。

（I）根据茎叶图分别计算有记号的两种鱼的平均数，并估计池塘中两种鱼的数量。

（II）随机从池塘中逐只有放回地捕出3只鱼，求恰好是1只金鱼2只红鲫鱼的概率。