已知，则等于

　    A．　　　             B．　　　             C．5　　                    D．25　

已知集合，，则等于

       A．    B．       C．     D．

复数等于

       A．              B．                            C．                  D．

设函数．

       （Ⅰ）当时，求函数的图象在点处的切线方程；

       （Ⅱ）已知，若函数的图象总在直线的下方，求的取值范围；

       （Ⅲ）记为函数的导函数．若，试问：在区间上是否存在（）个正数…，使得成立？请证明你的结论．

如图，点为坐标原点，直线经过抛物线的焦点．

（Ⅰ）若点到直线的距离为，求直线的方程；

       （Ⅱ）设点A是直线与抛物线在第一象限的交点．点B是以点为圆心,为半径的圆与轴负半轴的交点．试判断直线与抛物线的位置关系，并给出证明．

某学校为调查高三年学生的身高情况，按随机抽样的方法抽取80名学生，得到男生身高情况的频率分布直方图（图（1））和女生身高情况的频率分布直方图（图（2））．已知图（1）中身高在170 ~175cm的男生人数有16人．

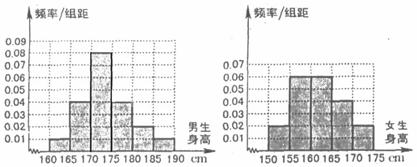
       图（1）                       图（2）

       （Ⅰ）试问在抽取的学生中，男、女生各有多少人？

       （Ⅱ）根据频率分布直方图，完成下列的2×2列联表，并判断能有多大（百分几）的把握认为“身高与性别有关”?

       （Ⅲ）在上述80名学生中，从身高在170～175cm之间的学生中按男、女性别分层抽样的方法，抽出5人，从这5人中选派3人当旗手，求3人中恰好有一名女生的概率．

        参考公式：

       参考数据：

设的三个内角所对的边分别为．已知．

       （Ⅰ）求角Ａ的大小；

       （Ⅱ）若，求的最大值．

如图1，在正方形中，，是边的中点，是边上的一点，对角线分别交、于、两点．将折起，使重合于点，构成如图2所示的几何体．

       （Ⅰ）求证：面；

（Ⅱ）试探究：在图1中，在什么位置时，能使折起后的几何体中／／平面，并给出证明．

等比数列的各项均为正数，且．

       （Ⅰ）求数列的通项公式；

       （Ⅱ）设，求数列的前项和．

设圆：，记为圆内部（不含边界）的整点的个数，其中整点是指横、纵坐标都是整数的点，则的所有可能值为__________________．