
科目: 来源: 题型:
若干个能唯一确定一个数列的量称为该数列的“基本量”,设{![]() }是公比为q的无穷等比数列,下列{
}是公比为q的无穷等比数列,下列{![]() }的四组量中,一定能成为该数列的“基本量”的是第 组。(写出所有符合要求的组号)
}的四组量中,一定能成为该数列的“基本量”的是第 组。(写出所有符合要求的组号)
①![]() 与
与![]() ②
②![]() 与
与![]() ③
③![]() 与
与![]() ④q与
④q与![]()
其中n为大于1的整数,![]() 为{
为{![]() }前n项和。
}前n项和。
查看答案和解析>>
科目: 来源: 题型:
(本题满分12)
已知数列{an}的前n项和为Sn,Sn=2-(![]() +1)an(n≥1).
+1)an(n≥1).
(Ⅰ)求证:数列{![]() }是等比数列;
}是等比数列;
(Ⅱ)设数列{2nan}的前n项和为Tn,An=![]() .试比较An与
.试比较An与![]() 的大小。
的大小。
查看答案和解析>>
科目: 来源: 题型:
如果有穷数列![]() (
(![]() 为正整数)满足
为正整数)满足![]() .即
.即![]() ,我们称其为“对称数列”例如,数列
,我们称其为“对称数列”例如,数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 与数列
与数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 都是“对称数列”.设
都是“对称数列”.设![]() 是项数为
是项数为![]() 的“对称数列”,并使得
的“对称数列”,并使得![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 依次为该数列中连续的前
依次为该数列中连续的前![]() 项,则数列
项,则数列![]() 的前
的前![]() 项和
项和![]() 可以是
可以是
⑴![]() ⑵
⑵![]() (3)
(3)![]()
其中正确命题的个数为 ( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,
, ![]() 。
。
(1)令![]() ,是否存在正整数
,是否存在正整数![]() ,使得对一切正整数
,使得对一切正整数![]() ,总有
,总有![]() ,若存在,求出
,若存在,求出![]() 的最小值;若不存在,说明理由。
的最小值;若不存在,说明理由。
(2)令 ![]() ,
,![]() 的前
的前![]() 项和为
项和为![]() , 求证:
, 求证:![]()
![]() 。
。
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,
若![]() ,
,
(1)求数列![]() 的通项公式;
的通项公式;
(2)令![]() ,是否存在正整数
,是否存在正整数![]() ,使得对一切正整数
,使得对一切正整数![]() ,总有
,总有![]() ,
,
若存在,求出![]() 的最小值;若不存在,说明理由。
的最小值;若不存在,说明理由。
查看答案和解析>>
科目: 来源: 题型:
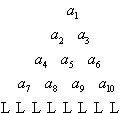 将正数数列
将正数数列![]() 中的所有项按每一行比上一行多一项的规则排成数表,如图所示。记表中各行的第一个数
中的所有项按每一行比上一行多一项的规则排成数表,如图所示。记表中各行的第一个数![]() 构成数列为
构成数列为![]() ,各行的最后一个数
,各行的最后一个数![]() 构成数列为
构成数列为![]() ,第
,第![]() 行所有数的和为
行所有数的和为![]()
![]() 。已知数列
。已知数列![]() 是公差为
是公差为![]() 的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数
的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式。
的通项公式。
(2)(理科)记![]()
![]() ,
,
求证:![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com