科目： 来源： 题型：
本小题满分12分
的内切圆与三边
的切点分别为
，已知
，内切圆圆心
，设点
的轨迹为
.
（1）求的方程；
（2）过点
的动直线
交曲线于不同的两点
（点
在
轴的上方），问在轴上是否存在一定点
（不与重合），使
恒成立，若存在，试求出点的坐标；若不存在，说明理由.
查看答案和解析>>
科目： 来源： 题型：
（本小题满分14分）
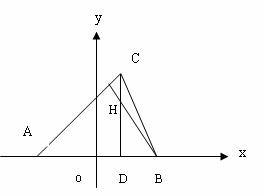
如图，在
,已知A(-
,0), B(,0), CD
AB于D, 
的垂心为H，且
（Ⅰ）求点H的轨迹方程;
（Ⅱ）若过定点F（0，2）的直线交曲线
于不同的两点
（点
在F,H之间），且满足
，求
的取值范围.
查看答案和解析>>
科目： 来源： 题型：
（本小题满分12分）
已知、分别是直线和上的两个动点，线段的长为，是的中点.
(1) 求动点的轨迹的方程.
(2) 过点作与轴不垂直的直线，交曲线于、两点,若在线段上存在点，使得以、为邻边的平行四边形是菱形，试求的取值范围.
查看答案和解析>>
科目： 来源： 题型：
（本小题满分12分）
已知实轴长为2a，虚轴长为2b的双曲线S的焦点在x轴上，直线是双曲线S的一条渐近线，而且原点O，点A（a，0）和点B（0，-b）使等式·成立.
（I）求双曲线S的方程；
（II）若双曲线S上存在两个点关于直线对称，求实数k的取值范围.
查看答案和解析>>
科目： 来源： 题型：
|
（本题满分14分）第（1）小题满分6分，第（2）小题满分8分。 如图1，，是某地一个湖泊的两条互相垂直的湖堤，线段和曲线段分别是湖泊中的一座栈桥和一条防波堤。为观光旅游的需要，拟过栈桥上某点分别修建与，平行的栈桥、，且以、为边建一个跨越水面的三角形观光平台。建立如图2所示的直角坐标系，测得线段的方程是，曲线段的方程是，设点的坐标为，记。（题中所涉及的长度单位均为米，栈桥和防波堤都不计宽度） （1）求的取值范围； （2）试写出三角形观光平台面积关于的函数解析式，并求出该面积的最小值。
查看答案和解析>> 科目： 来源： 题型： （本题满分18分）第（1）小题满分4分，第（2）小题满分8分，第（3）小题满分6分。 定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”。如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比。已知椭圆 若椭圆
如图：直线 查看答案和解析>> 科目： 来源： 题型： （满分18分）本题有2小题，第1小题9分，第2小题9分． 在中，、为定点，为动点，记、、的对边分别为、、，已知，． （1）证明：动点一定在某个椭圆上，并求出该椭圆的标准方程； （2）设点为坐标原点，过点作直线与（1）中的椭圆交于两点，若，求直线的方程． 查看答案和解析>> 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com版权声明：本站所有文章，图片来源于网络，著作权及版权归原作者所有，转载无意侵犯版权，如有侵权，请作者速来函告知，我们将尽快处理，联系qq：3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |
。
，判断
与
是否相似？如果相似，求出
写出与椭圆
的椭圆
的方程；若在椭圆
、
关于直线
对称，求实数
与两个“相似椭圆”
和
分别交于点
和点
，证明：