
科目: 来源: 题型:
(本小题满分12分)
某装置由两套系统M,N组成,只要有一套系统工作正常,该装置就可以正常工作。每套系统都由三种电子模块T1,T2,T3组成(如图所示已知T1,T2,T3正常工作的概率都是![]() ,且T1,T2,T3能否正常 工作相互独立.(注:对每一套系统或每一种电子模块而言,只要有电流通过就能正常工作.)
,且T1,T2,T3能否正常 工作相互独立.(注:对每一套系统或每一种电子模块而言,只要有电流通过就能正常工作.)
(I )分别求系统M,N正常工作的概率;
(II)设该装I中两套系统正常工作的套数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.

查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
在“环境保护低碳生活知识竞赛”第一环节测试中,设有A、B、C三道必答题,分值依次为20分、30分、50分.竞赛规定:若参赛选手连续两道题答题错误,则必答题总分记为零分;否则各题得分之和记为必答题总分.已知某选手回答A、B、C三道题正确的概率分别为![]() ,且回答各题时相互之间没有影响.
,且回答各题时相互之间没有影响.
(I)若此选手按A、B,C的顺序答题,求其必答题总分不小于80分的概率;
(II)若此选手可以自由选择答题顺序,求其必答题总分为50分的概率.
查看答案和解析>>
科目: 来源: 题型:
某工厂师徒二人各加工相同型号的零件2个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为![]() ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为![]()
(I)求徒弟加工2个零件都是精品的概率;
(II)求徒弟加工该零件的精品数多于师父的概率;
(III)设师徒二人加工出的4个零件中精品个数为![]() ,求
,求![]() 的分布列与均值E
的分布列与均值E![]() .
.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分高☆考♂资♀源*网)某工厂师徒二人各加工相同型号的零件2个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为![]() ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为![]() (I)求徒弟加工2个零件都是精品的概率;
(I)求徒弟加工2个零件都是精品的概率;
(II)求徒弟加工该零件的精品数多于师父的概率;
(III)设师徒二人加工出的4个零件中精品个数为![]() ,求
,求![]() 的分布列与均值E
的分布列与均值E![]()
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
在一个盒子中,放有标号分别为1,2,3的三张卡片,先从这个盒子中有放回地先后抽取两张卡片,设这两张卡片的号码分别为![]() 为坐标原点,
为坐标原点,![]() 记
记![]() 。
。
(1)求随机变量![]() 的最大值,并求事件“
的最大值,并求事件“![]() 取最大值”的概率;
取最大值”的概率;
(2)求![]() 的分布列及数学期望。
的分布列及数学期望。
查看答案和解析>>
科目: 来源: 题型:
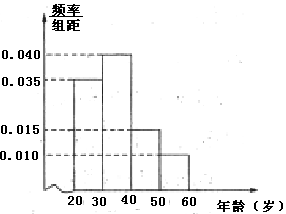
(本小题满分12分)某工厂有120名工人,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60]分组,其频率分布直方图如下图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试,已知各年龄段两项培训结业考试成绩优秀的人数如下表所示.假设两项培训是相互独立的,结业考试也互不影响。
| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20,30) | 30 | 18 |
| [30,40) | 36 | 24 |
| [40,50) | 12 | 9 |
| [50,60] | 4 | 3 |
(1)若用分层抽样法从全厂工人中抽取一个容量为40的样本,求各年龄段应分别抽取的人数,并估计全厂工人的平均年龄;
(2)随机从年龄段[20,30)和[30,40)中各抽取1人,设这两人中A、B两项培训结业考试成绩都优秀的人数为X,求X的分布列和数学期望。
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
某学校要用鲜花布置花圃中![]() 五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种
五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种
 不同颜色的鲜花可供任意选择.
不同颜色的鲜花可供任意选择.
(1)当![]() 区域同时用红色鲜花时,求布置花圃的不同
区域同时用红色鲜花时,求布置花圃的不同
方法的种数;
(2)求恰有两个区域用红色鲜花的概率;
(3)记![]() 为花圃中用红色鲜花布置的区域的个数,求随
为花圃中用红色鲜花布置的区域的个数,求随
机变量![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
某校一课题小组对南昌市工薪阶层对“楼市限购令”态度进行调查,抽调了50人,他们月收入频数分别表急对“楼市限购令”赞成人数如下表。
| 月收入 (单位:百元) |
|
|
|
|
|
|
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 3 | 1 |
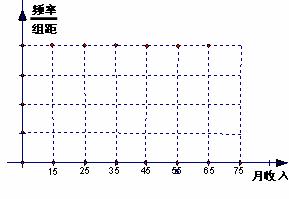
(1)完成下图的月收入频率分布直方图(注意填写纵坐标)及2×2列联表;
| 月收入不低于55百元人数 | 月收入低于55百元人数 | 合计 | |
| 赞成 |
|
| |
| 不赞成 |
|
| |
| 合计 |
(2)若从收入(单位:百元)在![]() 的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为
的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
下列四种说法:
(1)命题:“存在![]() ”的否定是“对任意
”的否定是“对任意![]() ”。
”。
(2)若直线a、b在平面α内的射影互相垂直,则![]()
(3)已知一组数据为20、30、40、50、60、70,则这组数据的众数、中位数、平均数的大小关系是:众数>中位数>平均数。
(4)已知回归方程![]() 则可估计x与y的增长速度之比约为
则可估计x与y的增长速度之比约为![]()
(5)若A(-2,3),B(3,-2),![]() 三点共线,则m的值为2。
三点共线,则m的值为2。
其中所有正确说法的序号是 。
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
 (1) 求这次铅球测试成绩合格的人数;
(1) 求这次铅球测试成绩合格的人数;
(2) 用此次测试结果估计全市毕业生的情况.若从今年的高中毕业生中随机抽取两名,记表示两人中成绩不合格的人数,求的分布列及数学期望;
(3) 经过多次测试后,甲成绩在8~10米之间,乙成绩在9.5~10.5米之间,现甲、乙各投掷一次,求甲比乙投掷远的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com