
科目: 来源: 题型:
(本小题满分12分) 在一块倾斜放置的矩形木块上钉着一个形如“等腰三角形”的五行铁钉,钉子之间留有空隙作为通道,自上而下第1行2个铁钉之间有1个空隙,第2行3个铁钉之间有2个空隙……第5行6个铁钉之间有5个空隙(如图).某人将一个玻璃球从第1行的空隙向下滚动,玻璃球碰到第2行居中的铁钉后以相等的概率滚入第2行的左空隙或右空隙,以后玻璃球按类似方式继续往下滚动,落入第5行的某一个空隙后,掉入木板下方相应的球槽.玻璃球落入不同球槽得到的分数ξ如图所示.
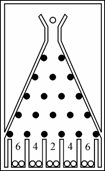 (Ⅰ)求
(Ⅰ)求![]() ;
;
(Ⅱ)若此人进行4次相同试验,求至少3次获得4分的概率.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
某公司在产品上市前需对产萵做检验,公司将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(I )若公司库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验.求至少有1件是合格品的概率;
(II)若该公司发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收,分别求出该商家抽出不合格产品为1件和2件的概率,并求该商家拒收这批产品的概率.
查看答案和解析>>
科目: 来源: 题型:
(本题满分12分)某幸运观众参加电视节目抽奖活动,抽奖规则是:在盒子里预先放有大小相同的5个小球,其中一个绿球,两个红球,两个白球.该观众依次从盒子里摸球,每次摸一个球(不放回),若累计摸到两个白球就停止摸球,否则直到将盒子里的球摸完才停止.规定:在球摸停止时,只有摸出红球才获得奖金,奖金数为摸出红球个数的1000倍(单位:元).
(Ⅰ)求该幸运观众摸三次球就停止的概率;
(Ⅱ)设x 为该幸运观众摸球停止时所得的奖金数(元),求x 的分布列和数学期望Ex.
查看答案和解析>>
科目: 来源: 题型:
给出定义:若![]() (其中
(其中![]() 为整数),则
为整数),则![]() 叫做离实数
叫做离实数![]() 最近的整数,记作
最近的整数,记作![]() ,在此基础上给出下列关于函数
,在此基础上给出下列关于函数![]() 的四个命题:
的四个命题:
①函数![]() =
=![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ;②函数
;②函数![]() =
=![]() 在
在![]() 上是增函数;
上是增函数;
③函数![]() =
=![]() 是周期函数,最小正周期为1;
是周期函数,最小正周期为1;
④函数![]() =
=![]() 的图象关于直线
的图象关于直线![]() (
(![]() )对称.
)对称.
其中正确命题的序号是__________
查看答案和解析>>
科目: 来源: 题型:
|
|
查看答案和解析>>
科目: 来源: 题型:
现有三枚外观一致的硬币,其中两枚是均匀硬币另一枚是不均匀的硬币,这枚不均匀的硬币抛出后正面出现的概率为![]() .现投掷这三枚硬币各1次,设
.现投掷这三枚硬币各1次,设![]() 为得到的正面个数,则随机变量
为得到的正面个数,则随机变量![]() 的数学期望
的数学期望![]() = ▲ .
= ▲ .
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
某车间在三天内,每天生产![]() 件某产品,其中第一天、第二天、第三天分别生产出了
件某产品,其中第一天、第二天、第三天分别生产出了![]() 件、
件、![]() 件、
件、![]() 件次品,质检部门每天要从生产的
件次品,质检部门每天要从生产的![]() 件产品中随机抽取
件产品中随机抽取![]() 件进行检测,若发现其中有次品,则当天的产品不能通过.
件进行检测,若发现其中有次品,则当天的产品不能通过.
(1)求第一天的产品通过检测的概率;
(2)记随机变量![]() 为三天中产品通过检测的天数,求
为三天中产品通过检测的天数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
一项"过关游戏"规则规定: 在第n 关要抛掷骰子n次, 若这n次抛掷所出现的点数之和大于![]() +1 (n∈N*), 则算过关.
+1 (n∈N*), 则算过关.
(1)求在这项游戏中第三关过关的概率是多少?
(2) 若规定n≤3, 求某人的过关数ξ的期望.
查看答案和解析>>
科目: 来源: 题型:
(本小题12分)
某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其
初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰,已知选手甲答题连续两次答错的概率为![]() ,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)
,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)
(I)求甲选手回答一个问题的正确率;
(Ⅱ)求选手甲可进入决赛的概率;
(Ⅲ)设选手甲在初赛中答题的个数为![]() ,试写出
,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望。
的数学期望。
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)某校选拔若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立。根据甲、
乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为![]() ,
,![]() ,
,![]() 。
。
第二次选拔,甲、乙、丙三人合格的概率依次为![]() ,
,![]() ,
,![]() 。
。
(1)求第一次选拔后甲、乙两人中只有甲合格的概率;
(2)分别求出甲、乙、丙三人经过前后两次选拔后合格的概率;
(3)设甲、乙、丙经过前后两次选拔后合格的人数为![]() ,求
,求![]() 的概率分布列及
的概率分布列及![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com