
科目: 来源: 题型:
在![]() 这
这![]() 个自然数中,任取
个自然数中,任取![]() 个不同的数.
个不同的数.
(1)求这![]() 个数中至少有
个数中至少有![]() 个是偶数的概率;
个是偶数的概率;
(2)求这![]() 个数和为18的概率;
个数和为18的概率;
(3)设![]() 为这
为这![]() 个数中两数相邻的组数(例如:若取出的数为
个数中两数相邻的组数(例如:若取出的数为![]() ,则有两组相邻的数
,则有两组相邻的数![]() 和
和![]() ,此时
,此时![]() 的值是
的值是![]() ).求随机变量
).求随机变量![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
某商场为促销设计了一个抽奖模型,一定数额的消费可以获得一张抽奖券,每张抽奖
券可以从一个装有大小相同的4个白球和2个红球的口袋中一次性摸出3个球,至少摸到一个红球则中奖.
(Ⅰ)求一次抽奖中奖的概率;
(Ⅱ)若每次中奖可获得10元的奖金,一位顾客获得两张抽奖券,求两次抽奖所得的奖
金额之和X(元)的概率分布和期望E(X).
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
某学校举行知识竞赛,第一轮选拔共设有A、B、C、D四个问题,规则如下:
每位参加者记分器的初始分均为10分,答对问题A、B、C、D分别加1分、2分、3分、6分,答错任一题减2分;
每回答一题,记分器显示累计分数,当累计分数小于8分时,答题结束,淘汰出局;当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
每位参加者按问题A、B、C、D顺序作答,直至答题结束。
假设甲同学对问题A、B、C、D回答正确的概率依次为![]() 、
、![]() 、
、![]() 、
、![]() ,且各题回答正确与否相互之间没有影响。
,且各题回答正确与否相互之间没有影响。
(Ⅰ)求甲同学能进入下一轮的概率;
(Ⅱ)用ξ表示甲同学本轮答题结束时答题的个数,求ξ的分布列和数学期望Εξ。
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为![]() .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。
(Ⅰ)求三位同学都没有中奖的概率;
(Ⅱ)求三位同学中至少有两位没有中奖的概率.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分13分,(I)小问5分,(II)小问8分)
在甲、乙等6个单位参加的一次“唱读讲传”演出活动中,每个单位的节目集中安排在一起,若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,……6),求:
(I)甲、乙两单位的演出序号至少有一个为奇数的概率;
(II)甲、乙两单位之间的演出单位个数![]() 的分布列与期望。
的分布列与期望。
查看答案和解析>>
科目: 来源: 题型:
(本小题共13分)
某同学参加3门课程的考试。假设该同学第一门课程取得优秀成绩的概率为![]() ,第二、第三门课程取得优秀成绩的概率分别为
,第二、第三门课程取得优秀成绩的概率分别为![]() ,
,![]() (
(![]() >
>![]() ),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
| ξ | 0 | 1 | 2 | 3 |
| P |
|
| b |
|
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求![]() ,
,![]() 的值;
的值;
(Ⅲ)求数学期望![]() ξ。
ξ。
查看答案和解析>>
科目: 来源: 题型:
(本题满分l4分)如图,一个小球从M处投入,通过管道自上而下落A或B或C。已知小球从每个叉口落入左右两个 管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.
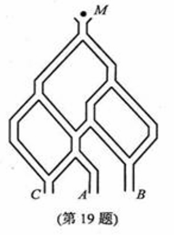 (I)已知获得l,2,3等奖的折扣率分别为50%,70%,90%.记随变量
(I)已知获得l,2,3等奖的折扣率分别为50%,70%,90%.记随变量![]() 为获得k(k=1,2,3)等奖的折扣率,求随机变量
为获得k(k=1,2,3)等奖的折扣率,求随机变量![]() 的分布列及期望
的分布列及期望![]() ;
;
(II)若有3人次(投入l球为l人次)参加促销活动,记随机变量![]() 为获得1等奖或2等奖的人次,求
为获得1等奖或2等奖的人次,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为![]() .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。
(Ⅰ)求甲中奖且乙、丙都没有中奖的概率;
(Ⅱ)求中奖人数ξ的分布列及数学期望Eξ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com