
科目: 来源: 题型:
(本题满分16分)
某车站有快慢两种车,始发站距终点站为![]() ,慢车匀速行驶到终点需
,慢车匀速行驶到终点需![]() ,快车比慢车晚发车
,快车比慢车晚发车![]() 且匀速行驶
且匀速行驶![]() 以后到达终点站,设慢车行驶时间为
以后到达终点站,设慢车行驶时间为![]() ,快、慢车行驶的路程分别为
,快、慢车行驶的路程分别为![]()
(1)分别写出![]() 的函数关系式并写出定义域;在同一坐标系中作出的图象
的函数关系式并写出定义域;在同一坐标系中作出的图象![]() 。
。
(2)两车中途何时相遇,此时距离始发站多远?
查看答案和解析>>
科目: 来源: 题型:
(本题满分15分)某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,
但实际出厂单价不低于51元
(1)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(2)设一次订购量为x个,零件的实际出厂单价为P元,写出函数P=f(x)的表达式
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个利润又是多少元?
(工厂售出一个零件的利润=实际出厂单价-成本)
查看答案和解析>>
科目: 来源: 题型:
(本小题满分16分)
某批发公司批发某商品,每件商品进价80元,批发价120元,该批发商为鼓励经销商批发,决定当一次批发量超过100个时,每多批发一个,批发的全部商品的单价就降低0.04元,但最低批发价不能低于102元.
(1)当一次订购量为多少个时,每件商品的实际批发价为102元?
(2)当一次订购量为![]() 个, 每件商品的实际批发价为
个, 每件商品的实际批发价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(3)根据市场调查发现,经销商一次最大定购量为![]() 个,则当经销商一次批发多少个零件时,该批发公司可获得最大利润.
个,则当经销商一次批发多少个零件时,该批发公司可获得最大利润.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
在经济学中,函数![]() 的边际函数
的边际函数![]() 定义为
定义为![]() .某公司每月最多生产100台报警系统装置,生产
.某公司每月最多生产100台报警系统装置,生产![]() 台(
台(![]() )的收入函数为
)的收入函数为![]() (单位:元),生产x台的成本函数为
(单位:元),生产x台的成本函数为![]() (单位:元),利润是收入与成本之差.
(单位:元),利润是收入与成本之差.
(1)求利润函数![]() 及边际利润函数
及边际利润函数![]() 的解析式,并指出它们的定义域;
的解析式,并指出它们的定义域;
(2)利润函数![]() 与边际利润函数
与边际利润函数![]() 是否具有相同的最大值?说明理由.
是否具有相同的最大值?说明理由.
查看答案和解析>>
科目: 来源: 题型:
通过研究学生的学习行为,心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所有的时间.讲授开始时,学生兴趣激增;中间有一段不太长的时间,学生的兴趣保持较理想的状态;随后学生的注意力开始分散.分析结果和实验表明,用f(x)表示学生接受概念的能力(f(x)的值愈大,表示接受的能力越强),x表示提出和讲授概念的时间(单位:分),可以有以下的公式
![]()
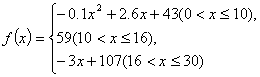
(1)开讲多少分钟后,学生的接受能力最强?能维持多长时间?
(2)开讲5分钟时和开讲20分钟时比较,学生的接受能力何时强些?
查看答案和解析>>
科目: 来源: 题型:
(12分)某地方政府为保护地方电子工业发展,决定对某一进口电子产品征收附加税.已知这种电子产品国内市场零售价为每件250元,每年可销售40万件,若政府增加附加税率为每百元收t元时,则每年销售量将减少![]() t万件.
t万件.
(1)将税金收入表示为征收附加税率的函数;
(2)若在该项经营中每年征收附加税金不低于600万元,那么附加税率应控制在什么范围?
查看答案和解析>>
科目: 来源: 题型:
若方程![]() -x-2=0的解在区间(n,n+1)内,n∈N*,根据表格中的数据,则n= ▲ .
-x-2=0的解在区间(n,n+1)内,n∈N*,根据表格中的数据,则n= ▲ .
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
查看答案和解析>>
科目: 来源: 题型:
(本题满分16分)
2010年上海世博会某国要建一座八边形(不一定为正八边形)的展馆区(如图),它的主体造型的平面图是由二个相同的矩形![]() 和
和![]() 构成的面积为
构成的面积为![]() m2的十字型地域,计划在正方形
m2的十字型地域,计划在正方形![]() 上建一座“观景花坛”,造价为
上建一座“观景花坛”,造价为![]() 元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为
元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为![]() 元/m2,再在四个空角(如
元/m2,再在四个空角(如![]() 等)上铺草坪,造价为
等)上铺草坪,造价为![]() 元/m2. 设总造价为
元/m2. 设总造价为![]() 元,
元,![]() 长为
长为![]() m.
m.
 (1)用
(1)用![]() 表示矩形
表示矩形![]() 的边
的边![]() 的长;
的长;
(1)试建立![]() 与
与![]() 的函数关系
的函数关系![]() ;
;
(2)当![]() 为何值时,
为何值时,![]() 最小?并求这个最小值.
最小?并求这个最小值.
查看答案和解析>>
科目: 来源: 题型:
(本题满分15分)
国家助学贷款是由财政贴息的信用贷款,旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费.每一年度申请总额不超过6000元.某大学2010届毕业生凌霄在本科期间共申请了![]() 元助学贷款,并承诺在毕业后
元助学贷款,并承诺在毕业后![]() 年内(按
年内(按![]() 个月计)全部还清.签约的单位提供的工资标准为第一年内每月
个月计)全部还清.签约的单位提供的工资标准为第一年内每月![]() 元,第
元,第![]() 个月开始,每月工资比前一个月增加
个月开始,每月工资比前一个月增加![]() 直到
直到![]() 元.凌霄同学计划前
元.凌霄同学计划前![]() 个月每个月还款额为
个月每个月还款额为![]() ,第
,第![]() 个月开始,每月还款额比上一月多
个月开始,每月还款额比上一月多![]() 元.
元.
(1)若凌霄恰好在第36个月(即毕业后三年)还清贷款,求![]() 的值;
的值;
(2)当![]() 时,凌霄同学将在第几个月还清最后一笔贷款?他当月工资的余额是否能满足每月
时,凌霄同学将在第几个月还清最后一笔贷款?他当月工资的余额是否能满足每月![]() 元的基本生活费?
元的基本生活费?
(参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com