(本小题满分16分)

已知常数，函数

（1）求的单调递增区间；

（2）若，求在区间上的最小值；

（3）是否存在常数，使对于任意时，

恒成立，若存在，求出的值；若不存在，说明理由。

若方程的解为，则满足的最大整数             ．

(本题满分16分)

已知函数(a为实常数).

(1)若，求证：函数在(1，+．∞)上是增函数；

(2)求函数在[1，e]上的最小值及相应的值；

(3)若存在，使得成立，求实数a的取值范围.

（本小题共14分）

设函数．

（I）求的单调区间；

（II）当0<a<2时，求函数在区间上的最小值．

（本小题满分14分）已知函数在与时都取得极值

       （Ⅰ）求的值与函数的单调区间；

       （Ⅱ）若对，不等式恒成立，求的取值范围。

（本小题满分14分）已知函数.

（Ⅰ）试判断函数f (x)的单调性并说明理由；

（Ⅱ）若对任意的，不等式组恒成立，求实数k的取值范围。

         给出下列5个命题：    .      /

①是函数在区间上为单调减函数的充要条件

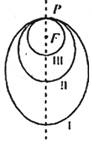②如图所示，“嫦娥探月卫星”沿地月转移轨道飞向月球，在月球附近一点P进入以月球球心F为一个焦点的椭圆叙道I绕月飞行，之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道II绕月飞行，最终卫星在P点第三次变轨进入以F为圆心的圆形轨道III绕月飞行,若用2c_l和2c₂分别表示椭圆轨道I和II的焦距，用2a1和2a2分别表示椭圆轨道I和II的长轴的长，则有a₁-c₁ = a₂-c₂;

③与它的反函数的图象若相交，则交点必在直线y= 上_；
④若,则；

⑤函数（e是自然对数的底数）的最小值为2.
其中所有真命题的代号有____________

下列说法：

       ①“”的否定是“”；

       ②函数的最小正周期是

       ③命题“函数处有极值，则”的否命题是真命题；

       ④上的奇函数，时的解析式是，则时的解析式为其中正确的说法是       。

（本小题满分14分）已知函数，

（Ⅰ）求的单调区间；（友情提示：）

（Ⅱ）求证：当时，；

（Ⅲ）当取什么值时，存在一次函数，使得对任意都有

，并求出的解析式.

设{}表示离最近的整数，即若_， ()，则．给出下列关于函数的四个命题：
①函数的定义域是R，值域是[0，]；
②函数的图像关于直线对称；
③函数是周期函数，最小正周期是1；
④函数是连续函数，但不可导．

 其中正确命题的序号为　　　　　．（写出所有你认为正确的序号）