
科目: 来源: 题型:
一位射击选手100发子弹的射击结果统计如下:
| 环数 | 10环 | 9环 | 8环 | 7环 | 6环 | 5环以下(含5环) |
| 频数 | 20 | 35 | 25 | 13 | 5 | 2 |
试根据以上统计数据估算:
(1)该选手一次射击射中8环以上(含8环)的概率;
(2)该选手射击2发子弹取得19环以上(含19环)的成绩的概率.
查看答案和解析>>
科目: 来源: 题型:
某先生居住在城镇的A处,准备开车在单位B处上班.若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图.(例如:A→C→D算作两个路段;路段AC发生堵车事件的概率为![]() ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为![]() ).
).
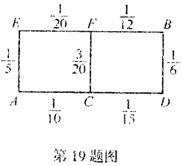
请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小.
查看答案和解析>>
科目: 来源: 题型:
某会议室用5盏灯照明,每盏灯各使用灯泡一只,且型号相同.假定每盏灯能否正常照明只与灯泡的寿命有关,该型号的灯泡寿命为1年以上的概率为![]() ,寿命为2年以上的概率为
,寿命为2年以上的概率为![]() ,从使用之日起每满1年进行一次灯泡更换工作,只更换已坏的灯泡,平时不换.
,从使用之日起每满1年进行一次灯泡更换工作,只更换已坏的灯泡,平时不换.
(1)在第一次灯泡更换工作中,求不需要换灯泡的概率和更换2只灯泡的概率;
(2)在第二次灯泡更换工作中,对其中的某一盏灯来说,求该盏灯需要更换灯泡的概率;
(3)当![]() ,
,![]() 时,求在第二次灯泡更换工作中,至少需要更换4只灯泡的概率(结果保留两个有效数字).
时,求在第二次灯泡更换工作中,至少需要更换4只灯泡的概率(结果保留两个有效数字).
查看答案和解析>>
科目: 来源: 题型:
三个元件![]() 正常工作的概率分别为
正常工作的概率分别为![]() ,将它们中某两个元件并联后再和第三个元件串联接入电路.
,将它们中某两个元件并联后再和第三个元件串联接入电路.

(1)在如图的电路中,电路不发生故障的概率是多少?
(2)三个元件连成怎样电路,才能使电路中不发生故障的概率最大?请画出此时电路图,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
有人玩掷硬币跳跳棋的游戏,已知硬币正反面出现概率均为![]() ,棋盘上标有第0站,第1站,第2站,…,第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次.若掷正面棋子向前跳一站(从k到k+1);若掷出反面,棋子向前跳二站(从k到k+2),直到棋子跳到第99站(胜利大本营)或跳到第100站(失败集中营)时,该游戏结束,设棋子跳到第n站的概率为
,棋盘上标有第0站,第1站,第2站,…,第100站.一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次.若掷正面棋子向前跳一站(从k到k+1);若掷出反面,棋子向前跳二站(从k到k+2),直到棋子跳到第99站(胜利大本营)或跳到第100站(失败集中营)时,该游戏结束,设棋子跳到第n站的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 及
及![]() 的值;
的值;
查看答案和解析>>
科目: 来源: 题型:
(本题13分)在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)
| 分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 合计 |
|
共有100个数据,将数据分组如右表:
(1)画出频率分布表,并画出频率分布直方图;
(2)估计纤度落在![]() 中的概率及纤度小于
中的概率及纤度小于![]() 的概率是多少?
的概率是多少?
(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
查看答案和解析>>
科目: 来源: 题型:
(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(![]() 吨)与
吨)与
相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
|
| 3 | 4 | 5 | 6 |
|
| 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式  ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com