
科目: 来源: 题型:
设函数![]() 为区间
为区间![]() 上的图像是连续不断的一条曲线,且恒有
上的图像是连续不断的一条曲线,且恒有![]() ,可以用随机模拟方法近似计算由曲线
,可以用随机模拟方法近似计算由曲线![]() 及直线
及直线![]() ,
,![]() ,
,![]() 所围成部分的面积S,先产生两组(每组
所围成部分的面积S,先产生两组(每组![]() 个)区间
个)区间![]() 上的均匀随机数
上的均匀随机数![]() 和
和![]() ,由此得到N个点(xi,yi)(
,由此得到N个点(xi,yi)(![]() =1,2,…,N).再数出其中满足yi≤f(xi
=1,2,…,N).再数出其中满足yi≤f(xi![]() 的点数
的点数![]() ,那么由随机模拟方法可得S的近似值为___________
,那么由随机模拟方法可得S的近似值为___________
查看答案和解析>>
科目: 来源: 题型:
设函数![]() 为区间
为区间![]() 上的图像是连续不断的一条曲线,且恒有
上的图像是连续不断的一条曲线,且恒有![]() ,可以用随机模拟方法计算由曲线
,可以用随机模拟方法计算由曲线![]() 及直线
及直线![]() ,
,![]() ,
,![]() 所围成部分的面积,先产生两组
所围成部分的面积,先产生两组![]() 每组
每组![]() 个,区间
个,区间![]() 上的均匀随机数
上的均匀随机数![]() 和
和![]() ,由此得到V个点
,由此得到V个点![]() 。再数出其中满足
。再数出其中满足![]() 的点数
的点数![]() ,那么由随机模拟方法可得S的近似值为___________
,那么由随机模拟方法可得S的近似值为___________
查看答案和解析>>
科目: 来源: 题型:
设y=f(x)为区间[0,1]上的连续函数,且恒有0≤f(x) ≤1,可以用随机模拟方法近似计算积分![]() ,先产生两组(每组N个)区间[0,1]上的均匀随机数
,先产生两组(每组N个)区间[0,1]上的均匀随机数![]() ,
,![]() …,
…,![]() 和
和![]() ,
,![]() …,
…,![]() ,由此得到N个点(
,由此得到N个点(![]() ,
,![]() )(i=1,2,…,N),在数出其中满足
)(i=1,2,…,N),在数出其中满足![]() ≤
≤![]() ((i=1,2,…,N))的点数
((i=1,2,…,N))的点数![]() ,那么由随机模拟方法可得积分
,那么由随机模拟方法可得积分![]() 的近似值为 .
的近似值为 .
查看答案和解析>>
科目: 来源: 题型:
(本小题满分13分)
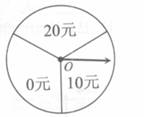
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费每满100元可以转动如图所示的圆盘一次,其中O为圆心,且标有20元、10元、0元的三部分区域面积相等,假定指针停在任一位置都是等可能的.当指针停在某区域时,返相应金额的优惠券。(例如:某顾客消费了218元,第一次转动获得了20元,第二次获得了10元,则其共获得了30元优惠券。)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.
(I)若顾客甲消费了128元,求他获得优惠券面额大于0元的概率?
(II)若顾客乙消费了280元,求他总共获得优惠券金额不低于20元的概率?
查看答案和解析>>
科目: 来源: 题型:
一只小蜜蜂在一个棱长为30的正方体玻璃容器内随机飞行,若蜜蜂在飞行过程中与正方体玻璃容器6个表面中至少有一个的距离不大于10,则就有可能撞到玻璃上而不安全;若始终保持与正方体玻璃容器6个表面的距离均大于10,则飞行是安全的,假设蜜蜂在正方体玻璃容器内飞行到每一位置可能性相同,那么蜜蜂飞行是安全的概率是
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com