
科目: 来源: 题型:
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知数列![]() 的前
的前![]() 项和
项和![]() 满足条件
满足条件![]() ,其中
,其中![]() .
.
(1)求证:数列![]() 成等比数列;
成等比数列;
(2)设数列![]() 满足
满足![]() .若
.若 ![]() , 求数列
, 求数列![]() 的前
的前![]() 项和.
项和.
查看答案和解析>>
科目: 来源: 题型:
(本题满分14分,其中第1小题6分,第2小题8分)
为了贯彻节能减排的理念,国家制定了家电能耗的节能标准.以某品牌的节能型冰箱为例,该节能型冰箱使用一天(24小时)耗电仅![]() 度,比普通冰箱约节省电能
度,比普通冰箱约节省电能![]() ,达到国家一级标准.经测算,每消耗100度电相当于向大气层排放
,达到国家一级标准.经测算,每消耗100度电相当于向大气层排放![]() 千克二氧化碳,而一棵大树在60年的生命周期内共可以吸收1吨二氧化碳.
千克二氧化碳,而一棵大树在60年的生命周期内共可以吸收1吨二氧化碳.
(1)一台节能型冰箱在一个月(按![]() 天不间断使用计算)中比普通冰箱相当于少向大气层排放多少千克的二氧化碳(精确到
天不间断使用计算)中比普通冰箱相当于少向大气层排放多少千克的二氧化碳(精确到![]() 千克)?
千克)?
(2)某小城市数千户居民现使用的都是普通冰箱. 在“家电下乡”补贴政策支持下,若每月月初都有150户居民“以旧换新”换购节能型冰箱,那么至少多少个月后(每月按30天不间断使用计算),该市所有新增的节能型冰箱少排放的二氧化碳的量可超过150棵大树在60年生命周期内共吸收的二氧化碳的量?
查看答案和解析>>
科目: 来源: 题型:
(本题满分16分)第(1)小题满分5分,第(2)小题满分5分,第(3)小题满分6分。
 各项均为正数的数列
各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() 。
。
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,数列
,数列![]() 满足
满足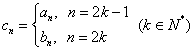 ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,当
,当![]() 为偶数时,求
为偶数时,求![]() ;
;
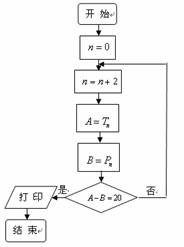
(3)若数列![]() ,甲同学利用第(2)问中的
,甲同学利用第(2)问中的![]() ,试图确定
,试图确定![]() 的值是否可以等于20?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由。
的值是否可以等于20?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由。
查看答案和解析>>
科目: 来源: 题型:
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知数列![]() 是首项
是首项![]() ,公比
,公比![]() 的等比数列,设
的等比数列,设![]() ,常数
,常数![]() ,数列
,数列![]() .
.
(1)求证:![]() 是等差数列;
是等差数列;
(2)若![]() 是递减数列,求t的最小值;
是递减数列,求t的最小值;
(3)是否存在正整数k,使![]() 重新排列后成等比数列?若存在,求k,t的值;若不
重新排列后成等比数列?若存在,求k,t的值;若不
存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
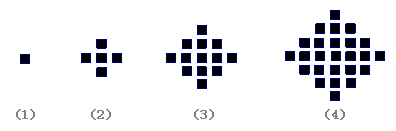
某少数民族的刺绣有着悠久的历史,图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,图案都是由小正方形构成,小正方形数越多刺绣越漂亮;现按同样的摆放规律刺绣,设第![]() 个图形包含
个图形包含![]() 个小正方形。则
个小正方形。则![]() .
.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)设数列{an}的前n项和为Sn,点(n,![]() )(n∈N*)均在函数y=3x-2的图像上。(Ⅰ)求数列{an}的通项公式;(Ⅱ)设bn=
)(n∈N*)均在函数y=3x-2的图像上。(Ⅰ)求数列{an}的通项公式;(Ⅱ)设bn=![]() ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<![]() 对所有n∈N*都成立的最小正整数m。
对所有n∈N*都成立的最小正整数m。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com