
科目: 来源: 题型:
(本小题满分16分)
两县城A和B相距20km,现计划在两县城外以AB为直径的半圆弧![]() 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在![]() 的中点时,对城A和城B的总影响度为0.065.
的中点时,对城A和城B的总影响度为0.065.
(1)按下列要求建立函数关系式:
(i)设![]() (rad),将
(rad),将![]() 表示成
表示成![]() 的函数;并写出函数的定义域. (5分)
的函数;并写出函数的定义域. (5分)
(ii)设![]() (km),将
(km),将![]() 表示成
表示成![]() 的函数;并写出函数的定义域. (5分)
的函数;并写出函数的定义域. (5分)
 (2)请你选用(1)中的一个函数关系确定垃圾处理厂的位置,使建在此处的垃圾处理厂对城A和城B的总影响度最小? (6分)
(2)请你选用(1)中的一个函数关系确定垃圾处理厂的位置,使建在此处的垃圾处理厂对城A和城B的总影响度最小? (6分)
查看答案和解析>>
科目: 来源: 题型:
(本小题满分16分)
已知函数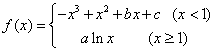 的图象过点
的图象过点![]() ,且在点
,且在点![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1) 求实数![]() 的值; (6分)
的值; (6分)
(2) 求![]() 在
在![]() (
(![]() 为自然对数的底数)上的最大值; (5分)
为自然对数的底数)上的最大值; (5分)
(3) 对任意给定的正实数![]() ,曲线
,曲线![]() 上是否存在两点
上是否存在两点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在![]() 轴上? (5分)
轴上? (5分)
查看答案和解析>>
科目: 来源: 题型:
如图是某市在城市改造中沿市内主干道修建的圆形休闲广场,圆心为![]() ,半径为100
,半径为100![]() .其与主干道一边所在
.其与主干道一边所在![]() 相切于点
相切于点![]() ,
,![]() 为上半圆弧上一点,过点
为上半圆弧上一点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() .市园林局计划在
.市园林局计划在![]() 内进行绿化,设
内进行绿化,设![]() 的面积为
的面积为![]() (单位:
(单位:![]() ).
).
(Ⅰ)设![]() ,将
,将![]() 表示成
表示成![]() 的函数;
的函数;
(Ⅱ)为使绿化的面积最大,试确定此时点![]() 的位置及其最大面积.
的位置及其最大面积.

查看答案和解析>>
科目: 来源: 题型:
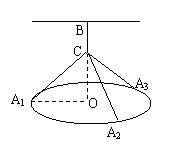
(本小题满分16分)如图所示:一吊灯的下圆环直径为4m,圆心为O,通过细绳悬挂在天花板上,圆环呈水平状态,并且与天花板的距离![]() 为2m,在圆环上设置三个等分点A1,A2,A3.点C为
为2m,在圆环上设置三个等分点A1,A2,A3.点C为![]() 上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等.设细绳的总长为ym.
上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等.设细绳的总长为ym.
(1)①设∠CA1O = ![]() (rad),将y表示成θ的函数关系式;
(rad),将y表示成θ的函数关系式;
②设CO=x m, 将y表示成x的函数关系式;
 (2)请你选用(1)中的一个函数关系确定BC的长使细绳总长y 最小.
(2)请你选用(1)中的一个函数关系确定BC的长使细绳总长y 最小.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分13分)如图所示,校园内计划修建一个矩形花坛并在花坛内装置两个相同的喷水器。已知喷水器的喷水区域是半径为5m的圆。问如何设计花坛的尺寸和两个喷水器的位置,才能使花坛的面积最大且能全部喷到水?

查看答案和解析>>
科目: 来源: 题型:
(本小题满分10分)已知某厂生产x件产品的成本为![]() (元).
(元).
(1)要使平均成本最低,应生产多少件产品?
(2)若产品以每件500元售出,要使利润最大,应生产多少件产品?
查看答案和解析>>
科目: 来源: 题型:
如图,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器,当这个正六棱柱容器的底面边长为 时,其容积最大.
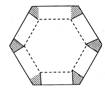 (第16题图)
(第16题图)
查看答案和解析>>
科目: 来源: 题型:
为了降低能源损耗,最近冀州市对新建住宅的屋顶和外墙都要求建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度![]() (单位:cm)满足关系:
(单位:cm)满足关系: ![]() ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设![]() 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式(注明定义域);
的表达式(注明定义域);
(2)隔热层修建多厚时,总费用![]() 达到最小.
达到最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com