（本小题满分12分）

如图，已知四棱锥P-ABCD的底面为等腰梯形，ABCD,ACBD，垂足为H，

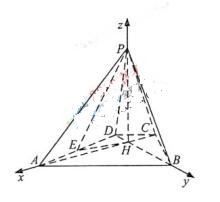PH是四棱锥的高 ，E为AD中点

证明：PEBC

若APB=ADB=60°，求直线PA与平面PEH所成角的正弦值

本小题满分12分，（I）小问5分，（II）小问7分）

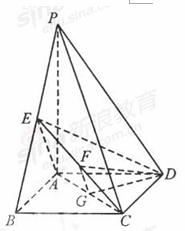
如题（19）图，四棱锥P-ABCD中，底面ABCD为矩形，PA底面ABCD，PA=AB=，点E是棱PB的中点。

求直线AD与平面PBC的距离；

若AD=，求二面角A-EC-D的平面角的余弦值。

（本小题共14分）

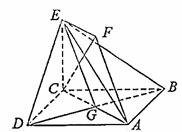     如图，正方形ABCD和四边形ACEF所在的平面互相垂直，CE⊥AC,EF∥AC,AB=，CE=EF=1.

（Ⅰ）求证：AF∥平面BDE；

（Ⅱ）求证：CF⊥平面BDE；

（Ⅲ）求二面角A-BE-D的大小。

（本大题满分13分）本题共有2个小题，第1小题满分5分，第2小题满分8分.

如图所示，为了制作一个圆柱形灯笼，先要制作4个全等的矩形骨架，总计耗用9.6米铁丝，骨架把圆柱底面8等份，再用S平方米塑料片制成圆柱的侧面和下底面（不安装上底面）.

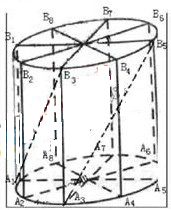(1)当圆柱底面半径取何值时，取得最大值？并求出该

最大值（结果精确到0.01平方米）;

（2）在灯笼内，以矩形骨架的顶点为点，安装一些霓虹灯，当灯笼的底面半径为0.3米时，求图中两根直线与所在异面直线所成角的大小（结果用反三角函数表示）

（本题满分15分）如图， 在矩形中，点分别在线段上，.沿直线将 翻折成，使平面.

（Ⅰ）求二面角的余弦值；

（Ⅱ）点分别在线段上，若沿直线将四边形向上翻折，使与重合，求线段的长。

题干

概率为。

（i）当点C在圆周上运动时，求的最大值；

（ii）记平面与平面所成的角为，当取最大值时，求的值。

（本小题满分12分）

如图△BCD与△MCD都是边长为2的正三角形，平面MCD平面BCD，AB平面BCD，。

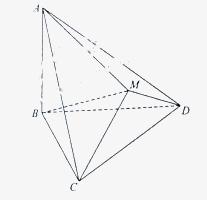求点A到平面MBC的距离；

求平面ACM与平面BCD所成二面角的正弦值。

（本小题满分12分）

如图，在长方体中，、分别是棱,上的点，,求异面直线与所成角的余弦值；证明平面

求二面角的正弦值。

（本小题满分14分）

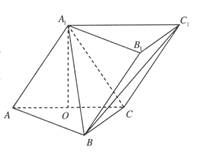如图，在三棱柱中，侧面底面ABC，，，且为AC中点。

证明：平面ABC；

求直线与平面所成角的正弦值；

在上是否存在一点E，使得平面

，若不存在，说明理由；若存在，确

定点E的位置。

（本小题满分14分）如图，斜三棱柱的底面是直角三角形，，点在底面上的射影恰好是的中点，且．

（Ⅰ）求证：平面平面；

（Ⅱ）求证：；

（Ⅲ）求二面角的大小.