
科目: 来源: 题型:
(本小题满分12分)
设二次函数![]() ,对任意实数
,对任意实数![]() ,有
,有![]() 恒成立;数列
恒成立;数列![]() 满足
满足![]() .
.
(1)求函数![]() 的解析式和值域;
的解析式和值域;
(2)试写出一个区间![]() ,使得当
,使得当![]() 时,数列
时,数列![]() 在这个区间上是递增数列,并说明理由;
在这个区间上是递增数列,并说明理由;
(3)已知![]() ,是否存在非零整数
,是否存在非零整数![]() ,使得对任意
,使得对任意![]() ,都有
,都有
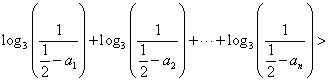
![]() 恒成立,若存在,求之;若不存在,说明理由.
恒成立,若存在,求之;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分14分)
现有甲,乙,丙,丁四名篮球运动员进行传球训练,由甲开始传球(即第一次传球是由甲传向乙或丙或丁),记第![]() 次传球球传回到甲的不同传球方式种数为
次传球球传回到甲的不同传球方式种数为![]() .
.
(1)试写出![]() ,
,![]() 并找出
并找出![]() 与
与![]() (
(![]() )的关系式;
)的关系式;
(2)求数列![]() 的通项公式;
的通项公式;
(3)证明:当![]() 时,
时, ![]()
![]() .
.
查看答案和解析>>
科目: 来源: 题型:
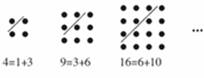
古希腊著名的毕达哥拉斯学派把1、3、6、10……这样的数称为“三角形数”,而把1、4、9 、16……这样的数称为“正方形数”。如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式为( )
①13=3+10; ②25=9+16; ③36=15+21; ④49=18+31;
⑤64=28+36
A.③⑤ B.②④⑤ C.②③④ D.①②③⑤
查看答案和解析>>
科目: 来源: 题型:
(本小题满分13分)
已知函数![]()
![]()
(1) 证明:函数![]() 的图像关于点
的图像关于点![]() 对称;
对称;
(2)若数列![]() 的通项公式为
的通项公式为![]()
![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设数列![]() 满足:
满足:![]()
![]() 。设
。设![]() 。若第(2)问中的
。若第(2)问中的![]() 满足对任意不小于
满足对任意不小于![]() 的正整数
的正整数![]() ,
,![]() 恒成立,试求正整数
恒成立,试求正整数![]() 的最大值。
的最大值。
查看答案和解析>>
科目: 来源: 题型:
(本小题满分14分)
已知数列![]() 满足
满足![]() ,首项为
,首项为![]() ;
;
(1)求数列![]() 的通项公式;
的通项公式;
(2)记![]() 数列
数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]() ;
;
(3)设数列![]() 满足
满足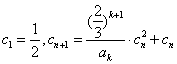 ,其中
,其中![]() 为一个给定的正整数,求证:当
为一个给定的正整数,求证:当![]() 时,恒有
时,恒有![]() .
.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分16分)
已知在直角坐标系中,![]() ,其中数列
,其中数列![]() 都是递增数列.
都是递增数列.
⑴若![]() ,判断直线
,判断直线![]() 与
与![]() 是否平行;
是否平行;
⑵若数列![]() 都是正项等差数列,设四边形
都是正项等差数列,设四边形![]() 的面积为
的面积为![]() ,
,
求证:![]() 也是等差数列;
也是等差数列;
⑶若![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,数列
,数列![]() 前8项依次递减,求满足条件的数列
前8项依次递减,求满足条件的数列![]() 的个数.
的个数.
查看答案和解析>>
科目: 来源: 题型:
一次研究性课堂上,老师给出函数![]() ,甲、乙、丙三位同学在研究此函数时分别给出命题:
,甲、乙、丙三位同学在研究此函数时分别给出命题:
甲:函数![]() ;
;
乙:若![]() 则一定有
则一定有![]() ;
;
丙:若规定![]() 恒成立
恒成立
你认为上述三个命题中正确的个数有 ( )
A.3个 B.2个 C.1个 D.0个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com