在实数集R中定义一种运算“*”，对任意为唯一确定的实数，且具有性质：

   （1）对任意    （2）对任意

   （3）对任意

       关于函数的性质，有如下说法：①函数的最小值为3；②函数为奇函数；③函数的单调递增区间为。其中所有正确说法的个数为                           （    ）

       A．0      B．1       C．2       D．3

（本小题满分12分）等差数列中，，前项和为，等比数列各项均为正数，，且，的公比

   （1）求与；

   （2）求

(本小题满分14分) 在平面直角坐标系上，设不等式组（）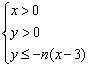

所表示的平面区域为，记内的整点（即横坐标和纵坐标均

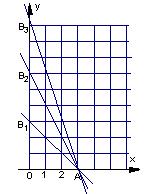为整数的点）的个数为.

（Ⅰ）求并猜想的表达式再用数学归纳法加以证明；

（Ⅱ）设数列的前_r项和为，数列的前_r项和,

是否存在自然数m？使得对一切，恒成立。若存在，

求出m的值，若不存在，请说明理由。

(本小题满分14分)已知正数数列{a_n }中，a₁ =2.若关于x的方程 （）对任意自然数n都有相等的实根．

(1)求a₂ ,a₃的值；

(2)求证（）．

（本小题满分14分）

已知数列中的相邻两项是关于的方程的两个根，且．

（I）求， ，，；    （II）求数列的前项和；

（Ⅲ）记，

，

求证：．

(本小题满分14分)

已知集合中的元素都是正整数，

且，对任意的且，有．

（Ⅰ）求证：；    （Ⅱ）求证：；

（Ⅲ）对于，试给出一个满足条件的集合．

（本小题满分13分）

若为集合且的子集，且满足两个条件：

①；

②对任意的，至少存在一个，使或.

则称集合组具有性质.

如图，作行列数表，定义数表中的第行第列的数为.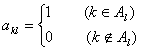

（Ⅰ）当时，判断下列两个集合组是否具有性质，如果是请画出所对应的表格，如果不是请说明理由；

集合组1：；

集合组2：.

（Ⅱ）当时，若集合组具有性质，请先画出所对应的行3列的一个数表，再依此表格分别写出集合；

（Ⅲ）当时，集合组是具有性质且所含集合个数最小的集合组，求的值及的最小值.（其中表示集合所含元素的个数）

（本小题满分13分）

若函数对任意的，均有，则称函数具有性质.

（Ⅰ）判断下面两个函数是否具有性质，并说明理由.

①；    ②.

（Ⅱ）若函数具有性质，且（），

求证：对任意有；

（Ⅲ）在（Ⅱ）的条件下，是否对任意均有.若成立给出证明，若不成立给出反例.

（本小题满分14分）

已知数列中，

（Ⅰ）求数列的通项；

（Ⅱ）求数列的前项和；

（Ⅲ）若存在,使得成立，求实数的取值范围.

（本小题满分12分）
已知数列{a_n}的各项均为正数，S_n为其前n项和；且S_n = 2 a_n -2（n∈N*）；

（1）求数列{a_n}的通项公式；
（2）设数列{b_n}的前n项和为T_n，且b_n= （n∈N*）；求证：对于任意的正整数n，总有T_n ＜2；
（3）在正数数列{c_n}中，设 (c_n) ⁿ⁺¹ = a_n+1（n∈N*）；求数列{c_n}中的最大项。