
科目: 来源: 题型:
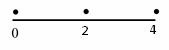
以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间![]() 对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等)。那么原闭区间
对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等)。那么原闭区间![]() 上(除两个端点外)的点,在第
上(除两个端点外)的点,在第![]() 次操作完成后(
次操作完成后(![]() ),恰好被拉到与4重合的点所对应的坐标为___________________________。[
),恰好被拉到与4重合的点所对应的坐标为___________________________。[
查看答案和解析>>
科目: 来源: 题型:
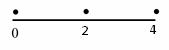
以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间![]() 对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等)。那么原闭区间
对应的线段,对折后(坐标4所对应的点与原点重合)再均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标1、3变成2,原来的坐标2变成4,等等)。那么原闭区间![]() 上(除两个端点外)的点,在第
上(除两个端点外)的点,在第![]() 次操作完成后(
次操作完成后(![]() ),恰好被拉到与4重合的点所对应的坐标为___________________________。[
),恰好被拉到与4重合的点所对应的坐标为___________________________。[
查看答案和解析>>
科目: 来源: 题型:
给出下列5个命题:
①![]() 是函数
是函数![]() 在区间(
在区间(![]() ,4]上为单调减函数的充要条件;
,4]上为单调减函数的充要条件;
 ②如图所示,“嫦娥探月卫星”沿地月转移轨道飞向月球,在月球附近一点P进入以月球球心F为一个焦点的椭圆轨道I绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道II绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道III绕月飞行,若用2Cl和2c2分别表示摘圆轨道I和II的焦距,用2a1和2a2分别表示椭圆轨道I和II的长轴的长,则有
②如图所示,“嫦娥探月卫星”沿地月转移轨道飞向月球,在月球附近一点P进入以月球球心F为一个焦点的椭圆轨道I绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道II绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道III绕月飞行,若用2Cl和2c2分别表示摘圆轨道I和II的焦距,用2a1和2a2分别表示椭圆轨道I和II的长轴的长,则有![]() ;
;
③函数![]() 与它的反函数
与它的反函数![]() 的图象若相交,则交点必在直线y =x上;
的图象若相交,则交点必在直线y =x上;
④己知函数![]() 在(O, 1)上满足,
在(O, 1)上满足,![]() ,贝U
,贝U![]() ;
;
⑤函数. ,
,![]() ,/为虚数单位)的最小值为2
,/为虚数单位)的最小值为2
其中所有真命题的代号是_____________________
查看答案和解析>>
科目: 来源: 题型:
(本小题满分13分)
已知函数![]() 定义在区间
定义在区间![]() ,对任意
,对任意![]() ,恒有
,恒有
![]() 成立,又数列
成立,又数列![]() 满足
满足![]()
(I)在(-1,1)内求一个实数t,使得![]()
(II)求证:数列![]() 是等比数列,并求
是等比数列,并求![]() 的表达式;
的表达式;
(III)设![]() ,是否存在
,是否存在![]() ,使得对任
,使得对任
意![]() ,
,![]() 恒成立?若存在,求出m的最小值;若不存在,请
恒成立?若存在,求出m的最小值;若不存在,请
说明理由。
查看答案和解析>>
科目: 来源: 题型:
|
|
查看答案和解析>>
科目: 来源: 题型:
(本小题共13分)
用![]() 表示不大于
表示不大于![]() 的最大整数.令集合
的最大整数.令集合![]() ,对任意
,对任意![]() 和
和![]() ,定义
,定义![]() ,集合
,集合![]() ,并将集合
,并将集合![]() 中的元素按照从小到大的顺序排列,记为数列
中的元素按照从小到大的顺序排列,记为数列![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() 的值;
的值;
(Ⅲ)求证:在数列![]() 中,不大于
中,不大于![]() 的项共有
的项共有![]() 项.
项.
查看答案和解析>>
科目: 来源: 题型:
已知定义在![]() 上的函数
上的函数 .给出下列结论:
.给出下列结论:
①函数![]() 的值域为
的值域为![]() ;
;
②关于![]() 的方程
的方程![]() 有
有![]() 个不相等的实数根;
个不相等的实数根;
③当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴围成的图形面积为
轴围成的图形面积为![]() ,则
,则![]() ;
;
④存在![]() ,使得不等式
,使得不等式![]() 成立,
成立,
其中你认为正确的所有结论的序号为______________________.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分16分)
已知数列![]() 满足
满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)对任意给定的![]() ,是否存在
,是否存在![]() (
(![]() )使
)使![]() 成等差数列?若存
成等差数列?若存
在,用![]() 分别表示
分别表示![]() 和
和![]() (只要写出一组);若不存在,请说明理由;
(只要写出一组);若不存在,请说明理由;
(3)证明:存在无穷多个三边成等比数列且互不相似的三角形,其边长为![]() .
.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分14分)
设数列![]() 是公差为
是公差为![]() 的等差数列,其前
的等差数列,其前![]() 项和为
项和为![]() .
.
(1)已知![]() ,
,![]() ,
,
(ⅰ)求当![]()
![]() 时,
时,![]() 的最小值;
的最小值;
(ⅱ)当![]()
![]() 时,求证:
时,求证:![]() ;
;
(2)是否存在实数![]() ,使得对任意正整数
,使得对任意正整数![]() ,关于
,关于![]() 的不等式
的不等式![]() 的最小正整数解为
的最小正整数解为![]() ?若存在,则求
?若存在,则求![]() 的取值范围;若不存在,则说明理由.
的取值范围;若不存在,则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com