（本题满分12分）某社区举办2011年西安世园会知识宣传活动，进行现场抽奖，抽奖规则是：盒中装有10张大小相同的精美卡片，卡片上分别印有“世园会会徽”或“长安花”（世园会吉祥物）图案，参加者从盒中一次抽取卡片两张，记录后放回。若抽到两张都是“长安花”卡即可获奖。

（Ⅰ）活动开始后，一位参加者问：盒中有几张“长安花”卡？主持人说：我只知道若从盒中抽两张都不是“长安花”卡的概率是，求抽奖者获奖的概率；

（Ⅱ）现有甲、乙、丙、丁四人每人抽奖一次，用表示获奖的人数，求的分布列及。

（本小题满分12分）

学校文艺队每个成员唱歌、跳舞至少会一门，已知会唱歌的人有5人，会跳舞的有3人. 现从中任选2人，其中至少一个人既会唱歌，又会跳舞的概率为.

（1）求选出的这2人中，都是既会唱歌，又会跳舞的概率；

（2）设选出的这2人中既会唱歌，又会跳舞的人数为，求的分布列及期望.

（本小题满分13分）

一个口袋中有2个白球和个红球（，且），每次从袋中摸出两个球（每次摸球后把这两个球放回袋中），若摸出的两个球颜色相同为中奖，否则为不中奖。

   （1）试用含的代数式表示一次摸球中奖的概率P；

   （2）若，求三次摸球恰有一次中奖的概率；

   （3）记三次摸球恰有一次中奖的概率为，当为何值时，最大。

（本小题满分12分）一个袋中装有四个形状大小完全相同的球，球的编号分别为1,2,3,4.

  （1）从袋中随机取出两个球，求取出的球的编号之和不大于4的概率；

  （2）先从袋中随机取一个球，该球的编号为m，将球放回袋中，然后再从袋中随机取一个球，该球的编号为n，求的概率.

（本小题满分12分）

甲、乙两同学组队参加学校举办的知识竞赛，其规则如下：比赛共设有“常识关”和“创新关”两关，甲冲 “常识关”，此关中有2道不同必答题，乙冲 “创新关”，此关中有3道不同必答题；如果“常识关”中的2道题都答对，则冲“常识关”成功且该团队获得单项奖励90元，否则无奖励；如果“创新关”中的3道题至少有2道题答对，则冲“创新关”成功且该团队获得单项奖励180元，否则无奖励，已知甲、乙回答每道题正确的概率分别为，；且两关之间互不影响，每道题回答正确与否相互独立．

 ( I ) 求此团队在这5道必答题中只有2道回答正确且没有获得任何奖励的概率；

(Ⅱ) 求此团队在这5道必答题中只有3道回答正确且获得180元奖金的概率．

(本小题满分13分)对某班级50名同学一年来参加社会实践的次数进行的调查统计，得到如下频率分布表：

根据上表信息解答以下问题：

(Ⅰ)从该班级任选两名同学，用η表示这两人参加社会实践次数之和，记“函数在区间，内有零点”的事件为，求发生的概率；

(Ⅱ)从该班级任选两名同学，用ξ表示这两人参加社会实践次数之差的绝对值，求随机变量ξ的分布列及数学期望Eξ.

(本小题满分12分) 从高三考试的学生中抽取20名学生成绩，分成六段得到如下的频率分布直方图，观察图形信息，回答下列问题：

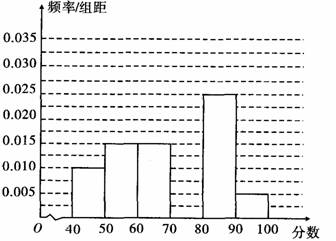
补全这个频率分布直方图；

利用频率分布直方图，估算这组数据的中位数（保留两位小数）；

从这20名学生中随机抽取2人，抽到的学生成绩在记分，在记分，在记分，用表示抽取结束后的总记分，

求的分布列及数学期望.

（本小题满分12分）

在一次考试中共有８道选择题，每道选择题都有４个选项，其中有且只有一个选项是正确的．评分标准规定：“每题只选一个选项，选对得５分，不选或选错得０分”．某考生已确定有4道题答案是正确的，其余题中：有两道只能分别判断２个选项是错误的，有一道仅能判断１个选项是错误的，还有一道因不理解题意只好乱猜，求：

（I）该考生得40分的概率；

（II）该考生得多少分的可能性最大？

（III）该考生所得分数的数学期望．

（本小题满分13分）

某食品厂为了检查一条自动包装流水线的生产情况，随机抽取该流水线上的40件产品作为样本称出它们的重量（单位：克），重量的分组区间为，，. . . ，.由此得到样本的频率分布直方图，如右图所示

（Ⅰ）根据频率分布直方图，求重量超过505克的产品数量；

（Ⅱ）在上述抽取的40件产品中任取2件，设为重量超过505

克的产品数量，求的分布列；

（Ⅲ）从流水线上任取5件产品，估计其中恰有2件产品的重量        超过505克的概率.

某班从6名干部中（其中男生4人，女生2人）选3人参加学校的义务劳动.

（1）设所选3人中女生人数为，求的分布列及；

（2）求男生甲或女生乙被选中的概率；

（3）在男生甲被选中的情况下，求女生乙也被选中的概率.