通过研究学生的学习行为，心理学家发现，学生的接受能力依赖于老师引入概念和描述问题所有的时间.讲授开始时，学生兴趣激增；中间有一段不太长的时间，学生的兴趣保持较理想的状态；随后学生的注意力开始分散.分析结果和实验表明，用f(x)表示学生接受概念的能力（f(x)的值愈大，表示接受的能力越强），x表示提出和讲授概念的时间（单位：分），可以有以下的公式

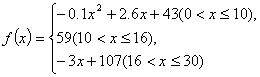
（1）开讲多少分钟后，学生的接受能力最强？能维持多长时间？

（2）开讲5分钟时和开讲20分钟时比较，学生的接受能力何时强些？

 （本小题满分12分）

在经济学中，函数的边际函数定义为．某公司每月最多生产100台报警系统装置，生产台（）的收入函数为（单位：元），生产x台的成本函数为（单位：元），利润是收入与成本之差．

(1)求利润函数及边际利润函数的解析式，并指出它们的定义域；

(2)利润函数与边际利润函数是否具有相同的最大值？说明理由.

（本题满分15分）某厂生产某种零件，每个零件的成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元，

但实际出厂单价不低于51元

（1）当一次订购量为多少个时，零件的实际出厂单价恰降为51元？

（2）设一次订购量为x个，零件的实际出厂单价为P元，写出函数P=f(x)的表达式

（3）当销售商一次订购500个零件时，该厂获得的利润是多少元？如果订购1000个利润又是多少元？

（工厂售出一个零件的利润＝实际出厂单价－成本）

经市场调查，某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天)的函数，且销售量近似满足g(t)=80-2t(件)，价格近似满足f(t)=20-|t-10|

(元).

(1)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数表达式；

(2)求该种商品的日销售额y的最大值与最小值.

（本题满分16分）

某车站有快慢两种车，始发站距终点站为，慢车匀速行驶到终点需，快车比慢车晚发车且匀速行驶以后到达终点站，设慢车行驶时间为，快、慢车行驶的路程分别为

（1）分别写出的函数关系式并写出定义域；在同一坐标系中作出的图象。

（2）两车中途何时相遇，此时距离始发站多远？

（本题满分15分）

某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律：每生产产品（百台），其总成本为（万元），其中固定成本为2.8万元，并且每生产1百台的生产成本为2万元（总成本=固定成本+生产成本）．销售收入（万元）满足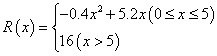，假定该产品产销平衡（即生产的产品都能卖掉），根据上述统计规律，请完成下列问题：

(1)写出利润函数的解析式（利润=销售收入—总成本）

(2)工厂生产多少台产品时，可使盈利最多？

为了保护环境，发展低碳经济，某单位在国家科研部门的支持下，进行技术攻关，采用了新工艺，把二氧化碳转化为一种可利用的化工产品．已知该单位每月的处理量最少为400吨，最多为600吨，月处理成本（元）与月处理量（吨）之间的函数关系可近似表示为：，且每处理一吨二氧化碳得到可利用的化工产品价值为100元

（1）若月处理成本不超过105000元，求月处理量的范围 ；

（2）该单位每月能否获利？如果获利，求出最大利润；如果不获利，则国家至少需要补贴多少元才能使该单位不亏损？

为了保护环境，发展低碳经济，某单位在国家科研部门的支持下，进行技术攻关，采用了新工艺，把二氧化碳转化为一种可利用的化工产品．已知该单位每月的处理量最少为400吨，最多为600吨，月处理成本（元）与月处理量（吨）之间的函数关系可近似表示为：，且每处理一吨二氧化碳得到可利用的化工产品价值为100元 

（1）若月处理成本不超过105000元，求月处理量的范围 ；

（2）该单位每月能否获利？如果获利，求出最大利润；如果不获利，

则国家至少需要补贴多少元才能使该单位不亏损？

（14分）在经济学中，函数的边际函数为，定义为，某公司每月最多生产100台报警系统装置。生产台的收入函数为（单位元），其成本函数为（单位元），利润等于收入与成本之差.

①求出利润函数及其边际利润函数；

②求出的利润函数及其边际利润函数是否具有相同的最大值；

③你认为本题中边际利润函数最大值的实际意义.

（本小题12分）

某企业为适应市场需求，准备投入资金16万元生产W和R型两种产品。经市场预测，生产W型产品所获利润（万元）与投入资金（万元）成正比例关系，且当投入资金为6万元时，可获利润1.5万元。生产R型产品所获利润（万元）与投入资金（万元）满足关系,为获得最大总利润，问生产W、R型产品各应投入资金多少万元？获得的最大总利润是多少？