
科目: 来源: 题型:
(本小题满分12分)
已知某企业原有员工2000人,每人每年可为企业创利3.5万元.为应对国际金融危机给企业带来的不利影响,该企业实施“优化重组,分流增效”的策略,分流出一部分员工待岗.为维护生产稳定,该企业决定待岗人数不超过原有员工的5%,并且每年给每位待岗员工发放生活补贴0.5万元.据评估,当待岗员工人数x不超过原有员工1%时,留岗员工每人每年可为企业多创利(1-![]() )万元;当待岗员工人数x超过原有员工1%时,留岗员工每人每年可为企业多创利0.9万元.为使企业年利润最大,应安排多少员工待岗?
)万元;当待岗员工人数x超过原有员工1%时,留岗员工每人每年可为企业多创利0.9万元.为使企业年利润最大,应安排多少员工待岗?
查看答案和解析>>
科目: 来源: 题型:
右图给出了某种豆类生长枝数![]() (枝)与时间
(枝)与时间![]() (月)的散点图,那么此种豆类生长枝数与时间的关系用下列函数模型近似刻画最好的是………………………………………………………………( )
(月)的散点图,那么此种豆类生长枝数与时间的关系用下列函数模型近似刻画最好的是………………………………………………………………( )
(A)![]() ; (B)
; (B)![]() ; (C)
; (C)![]() ; (D)
; (D)![]() .
.

查看答案和解析>>
科目: 来源: 题型:
(本题满分14分)
如图,在一条笔直的高速公路![]() 的同旁有两个城镇
的同旁有两个城镇![]() ,它们与
,它们与![]() 的距离分别是
的距离分别是![]() 与
与![]() ,
,![]() 在
在![]() 上的射影
上的射影![]() 之间距离为
之间距离为![]() ,现计划修普通公路把这两个城镇与高速公路相连接,若普通公路造价为
,现计划修普通公路把这两个城镇与高速公路相连接,若普通公路造价为![]() 万元/
万元/![]() ;而每个与高速公路连接的立交出入口修建费用为
;而每个与高速公路连接的立交出入口修建费用为![]() 万元.设计部门提交了以下三种修路方案:
万元.设计部门提交了以下三种修路方案:
 方案①:两城镇各修一条普通公路到高速公路,并各修一个立交出入口;
方案①:两城镇各修一条普通公路到高速公路,并各修一个立交出入口;
方案②:两城镇各修一条普通公路到高速公路上某一点![]() ,并
,并
在![]() 点修一个公共立交出入口;
点修一个公共立交出入口;
方案③:从![]() 修一条普通公路到
修一条普通公路到![]() ,再从
,再从![]() 修一条普通公路到
修一条普通公路到
高速公路,也只修一个立交出入口.
请你为这两个城镇选择一个省钱的修路方案.
查看答案和解析>>
科目: 来源: 题型:
(本题满分14分)
如图,在一条笔直的高速公路![]() 的同旁有两个城镇
的同旁有两个城镇![]() ,它们与
,它们与![]() 的距离分别是
的距离分别是![]() 与
与![]() ,
,![]() 在
在![]() 上的射影
上的射影![]() 之间距离为
之间距离为![]() ,现计划修普通公路把这两个城镇与高速公路相连接,若普通公路造价为
,现计划修普通公路把这两个城镇与高速公路相连接,若普通公路造价为![]() 万元/
万元/![]() ;而每个与高速公路连接的立交出入口修建费用为
;而每个与高速公路连接的立交出入口修建费用为![]() 万元.设计部门提交了以下三种修路方案:
万元.设计部门提交了以下三种修路方案:
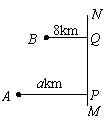 方案①:两城镇各修一条普通公路到高速公路,并各修一个立交出入口;
方案①:两城镇各修一条普通公路到高速公路,并各修一个立交出入口;
方案②:两城镇各修一条普通公路到高速公路上某一点![]() ,并
,并
在![]() 点修一个公共立交出入口;
点修一个公共立交出入口;
方案③:从![]() 修一条普通公路到
修一条普通公路到![]() ,再从
,再从![]() 修一条普通公路到
修一条普通公路到
高速公路,也只修一个立交出入口.
请你为这两个城镇选择一个省钱的修路方案.
查看答案和解析>>
科目: 来源: 题型:
(本题满分12分)
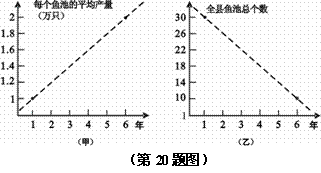 某县畜牧水产局连续6年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图:
某县畜牧水产局连续6年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图:
甲图调查表明:每个鱼池平均产量直线上升,从第1年1万只鳗鱼上升到第6年2万只. 乙图调查表明:全县鱼池总个数直线下降,由第1年30个减少到第6年10个.
请你根据提供的信息说明:
(Ⅰ)第5年全县鱼池的个数及全县出产的鳗鱼总数.
(Ⅱ)哪一年的规模(即总产量)最大?说明理由.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分16分)
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点。已知AB=3米,AD=2米。
(I)设![]() (单位:米),要使花坛AMPN的面积大于32平方米,求
(单位:米),要使花坛AMPN的面积大于32平方米,求![]() 的取值范围;
的取值范围;
|
并求出最大面积。
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
某企业科研课题组计划投资研发一种新产品,根据分析和预测,能获得10万元~1000万元的投资收益.企业拟制定方案对课题组进行奖励,奖励方案为:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金也不超过投资收益的20%,并用函数y= f(x)模拟这一奖励方案.
(Ⅰ)试写出模拟函数y= f(x)所满足的条件;
(Ⅱ)试分析函数模型y= 4lgx-3是否符合奖励方案的要求?并说明你的理由.
查看答案和解析>>
科目: 来源: 题型:
(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
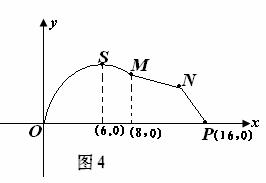
如图4,某市拟在长为16km的道路OP的一侧修建一条自行车赛道,赛道的前一部分为曲线OSM,该曲线段为函数![]() 的图像,且图像的最高点为
的图像,且图像的最高点为![]() .赛道的后一段为折线段MNP,为保证参赛队员的安全,限定
.赛道的后一段为折线段MNP,为保证参赛队员的安全,限定![]() .
.
(1)求实数![]() 的值以及M、P两点之间的距离;
的值以及M、P两点之间的距离;
(2)联结MP,设![]() ,试求出用
,试求出用![]() 的解析式;
的解析式;
(3)应如何设计,才能使折线段MNP最长?
查看答案和解析>>
科目: 来源: 题型:
(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
如图4,某市拟在长为16km的道路OP的一侧修建一条自行车赛道,赛道的前一部分为曲线OSM,该曲线段为函数![]() 的图像,且图像的最高点为
的图像,且图像的最高点为![]() .赛道的后一段为折线段MNP,为保证参赛队员的安全,限定
.赛道的后一段为折线段MNP,为保证参赛队员的安全,限定![]() .
.

(1)求实数![]() 的值以及M、P两点之间的距离;
的值以及M、P两点之间的距离;
(2)联结MP,设![]() ,试求出用
,试求出用![]() 的解析式;
的解析式;
(3)求函数y的最大值.
查看答案和解析>>
科目: 来源: 题型:
某人从2010年9月1日起,每年这一天到银行存款一年定期1万元,且每年到期的存款将本和利再存入新一年的一年定期,若一年定期存款利率![]() 保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为 【 】
保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为 【 】
A. 11314元 B. 53877元 C. 11597元 D.63877元
三、解答题(本题满分85分)本大题共有5题,解答下列各题必须在答题纸的规定区域(对
应的题号)内写出必要的步骤.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com