
科目: 来源: 题型:
若方程![]() -x-2=0的解在区间(n,n+1)内,n∈N*,根据表格中的数据,则n= ▲ .
-x-2=0的解在区间(n,n+1)内,n∈N*,根据表格中的数据,则n= ▲ .
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
查看答案和解析>>
科目: 来源: 题型:
(本题满分16分)
2010年上海世博会某国要建一座八边形(不一定为正八边形)的展馆区(如图),它的主体造型的平面图是由二个相同的矩形![]() 和
和![]() 构成的面积为
构成的面积为![]() m2的十字型地域,计划在正方形
m2的十字型地域,计划在正方形![]() 上建一座“观景花坛”,造价为
上建一座“观景花坛”,造价为![]() 元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为
元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为![]() 元/m2,再在四个空角(如
元/m2,再在四个空角(如![]() 等)上铺草坪,造价为
等)上铺草坪,造价为![]() 元/m2. 设总造价为
元/m2. 设总造价为![]() 元,
元,![]() 长为
长为![]() m.
m.
 (1)用
(1)用![]() 表示矩形
表示矩形![]() 的边
的边![]() 的长;
的长;
(1)试建立![]() 与
与![]() 的函数关系
的函数关系![]() ;
;
(2)当![]() 为何值时,
为何值时,![]() 最小?并求这个最小值.
最小?并求这个最小值.
查看答案和解析>>
科目: 来源: 题型:
(本题满分15分)
国家助学贷款是由财政贴息的信用贷款,旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费.每一年度申请总额不超过6000元.某大学2010届毕业生凌霄在本科期间共申请了![]() 元助学贷款,并承诺在毕业后
元助学贷款,并承诺在毕业后![]() 年内(按
年内(按![]() 个月计)全部还清.签约的单位提供的工资标准为第一年内每月
个月计)全部还清.签约的单位提供的工资标准为第一年内每月![]() 元,第
元,第![]() 个月开始,每月工资比前一个月增加
个月开始,每月工资比前一个月增加![]() 直到
直到![]() 元.凌霄同学计划前
元.凌霄同学计划前![]() 个月每个月还款额为
个月每个月还款额为![]() ,第
,第![]() 个月开始,每月还款额比上一月多
个月开始,每月还款额比上一月多![]() 元.
元.
(1)若凌霄恰好在第36个月(即毕业后三年)还清贷款,求![]() 的值;
的值;
(2)当![]() 时,凌霄同学将在第几个月还清最后一笔贷款?他当月工资的余额是否能满足每月
时,凌霄同学将在第几个月还清最后一笔贷款?他当月工资的余额是否能满足每月![]() 元的基本生活费?
元的基本生活费?
(参考数据:![]() )
)
查看答案和解析>>
科目: 来源: 题型:
(本小题14分)
已知某种稀有矿石的价值![]() (单位:元)与其重量
(单位:元)与其重量![]() (单位:克)的平方成正比,且
(单位:克)的平方成正比,且![]() 克该种矿石的价值为
克该种矿石的价值为![]() 元。
元。
⑴写出![]() (单位:元)关于
(单位:元)关于![]() (单位:克)的函数关系式;
(单位:克)的函数关系式;
⑵若把一块该种矿石切割成重量比为![]() 的两块矿石,求价值损失的百分率;
的两块矿石,求价值损失的百分率;
⑶把一块该种矿石切割成两块矿石时,切割的重量比为多少时,价值损失的百分率最大。
(注:价值损失的百分率![]() ;在切割过程中的重量损耗忽略不计)
;在切割过程中的重量损耗忽略不计)
查看答案和解析>>
科目: 来源: 题型:
 (本小题满分15分)为了研究某种药物,用小白鼠进行试验,发现药物在血液内的浓度与时间的关系因使用方式的不同而不同。若使用注射方式给药,则在注射后的3小时内,药物在白鼠血液内的浓度
(本小题满分15分)为了研究某种药物,用小白鼠进行试验,发现药物在血液内的浓度与时间的关系因使用方式的不同而不同。若使用注射方式给药,则在注射后的3小时内,药物在白鼠血液内的浓度![]() 与时间
与时间![]() 满足关系式:
满足关系式:![]() ,若使用口服方式给药,则药物在白鼠血液内的浓度
,若使用口服方式给药,则药物在白鼠血液内的浓度![]() 与时间
与时间![]() 满足关系式:
满足关系式: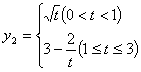 。现对小白鼠同时进行注射和口服该种药物,且注射药物和口服药物的吸收与代谢互不干扰。
。现对小白鼠同时进行注射和口服该种药物,且注射药物和口服药物的吸收与代谢互不干扰。
(1)若![]() ,求3小时内,该小白鼠何时血液中药物的浓度最高,并求出最大值
,求3小时内,该小白鼠何时血液中药物的浓度最高,并求出最大值
(2)若使小白鼠在用药后3小时内血液中的药物浓度不低于4,求正数![]() 的取值范围
的取值范围
查看答案和解析>>
科目: 来源: 题型:
(本题满分15分)图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,其中四边形ABCD是矩形,弧CmD是半圆,凹槽的横截面的周长为4.已知凹槽的强度与横截面的面积成正比,比例系数为![]() ,设AB=2x,BC=y.
,设AB=2x,BC=y.
(Ⅰ)写出y关于x函数表达式,并指出x的取值范围;
(Ⅱ)求当x取何值时,凹槽的强度最大.

查看答案和解析>>
科目: 来源: 题型:
某国由于可耕地面积少,计划从今年起的五年填湖围造一部分生产和生活用地,若填湖飞、购置排水设备费等所需经费与当年所填湖造地面积![]() (亩)的平方成长正比,其比例系数为
(亩)的平方成长正比,其比例系数为![]() ,设每亩水面的年平均经济效益为
,设每亩水面的年平均经济效益为![]() 元,填湖造地后的每亩土地的年平均收益为
元,填湖造地后的每亩土地的年平均收益为![]() 元(其中
元(其中![]() 均为常数且
均为常数且![]() )(1)若按计划填湖造地,且使得今年的收益不少于支出,试求所填面积
)(1)若按计划填湖造地,且使得今年的收益不少于支出,试求所填面积![]() 的最大值;(支出=造田的所需经费+水面经济收益)(2)如果填湖造地面积按每年1%的速度减少,为保证水面的蓄洪能力和环保要求,填湖造地的总面积不能超过现有水面面积的25%,求今年填湖造地的面积最多只能占现有水面的百分之几。注:根据下列近似值进行计算:
的最大值;(支出=造田的所需经费+水面经济收益)(2)如果填湖造地面积按每年1%的速度减少,为保证水面的蓄洪能力和环保要求,填湖造地的总面积不能超过现有水面面积的25%,求今年填湖造地的面积最多只能占现有水面的百分之几。注:根据下列近似值进行计算:
![]()
查看答案和解析>>
科目: 来源: 题型:
(本小题满分14分)
因发生意外交通事故,一辆货车上的某种液体泄漏到一渔塘中.为了治污,根据环保部门的建议,现决定在渔塘中投放一种可与污染液体发生化学反应的药剂.已知每投放![]() ,且
,且![]() 个单位的药剂,它在水中释放的浓度
个单位的药剂,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (天)变化的函数关系式近似为
(天)变化的函数关系式近似为![]() ,其中
,其中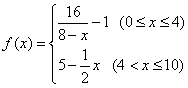 .
.
若多次投放,则某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和.根据经验,
当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.
(Ⅰ)若一次投放4个单位的药剂,则有效治污时间可达几天?
(Ⅱ)若第一次投放2个单位的药剂,6天后再投放![]() 个单位的药剂,要使接下来的4天中能够持续有效治污,试求
个单位的药剂,要使接下来的4天中能够持续有效治污,试求![]() 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据:![]() 取1.4).
取1.4).
查看答案和解析>>
科目: 来源: 题型:
(本题满分14分)
 某地有三家工厂,分别位于矩形ABCD的顶点A、B及CD的中点P处,已知AB=20km,BC=10km,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A、B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP,设排污管道的总长为ykm。
某地有三家工厂,分别位于矩形ABCD的顶点A、B及CD的中点P处,已知AB=20km,BC=10km,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A、B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP,设排污管道的总长为ykm。
(1)按下列要求写出函数关系式:
①设∠BAO=θ(rad),将y表示成θ的函数关系式;
②设OP=x(km),将y表示成x的函数关系式;
(2)请你选用(1)中的一个函数关系式,确定污水处理厂的位置,使三条排污管道总长度最短
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com