
科目: 来源: 题型:
(12分)随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示.
(1)根据茎叶图判断哪个班的平均身高较高;
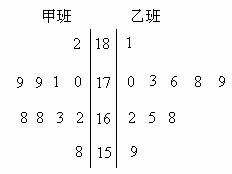 (2)计算甲班的样本方差
(2)计算甲班的样本方差
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)右面的表格是一组实验的统计数据:
| x | 0 | 1 | 2 | 3 |
| y | 1 | 2 | 3 | 0 |
(1) 求线性回归方程![]() ?
?
(2) 填写残差分布表.并计算残差的均值![]() .
.
(3) 求x对y的贡献率![]() ?并说明回归直线方程拟合效果.
?并说明回归直线方程拟合效果.
(备用公式: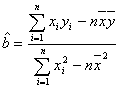 ;
;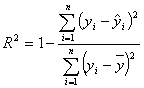 )
)
查看答案和解析>>
科目: 来源: 题型:
(本小题满分13分) 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;(2)请求出y关于x的线性回归方程![]() =
=![]() ;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(用最小二乘法求线性回归方程系数公式  .)
.)
查看答案和解析>>
科目: 来源: 题型:
在调查男女乘客是否晕机的情况中,已知男乘客晕机为28人,不会晕机的也是28人,而女乘客晕机为28人,不会晕机的为56人,
(1)根据以上数据建立一个![]() 的列联表;
的列联表;
(2)能否在犯错误的概率不超过0.05的前提下认为晕机与性别有关系?
(可能用到的公式:![]() ,可能用到数据:
,可能用到数据:![]() )
)
查看答案和解析>>
科目: 来源: 题型:
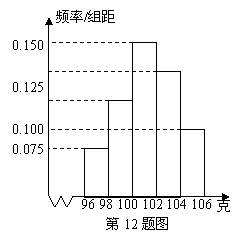
某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98],[98,100],[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( ).
A. 90 B. 75 C. 60 D. 45
查看答案和解析>>
科目: 来源: 题型:
(本小题满分13分)为了研究化肥对小麦产量的影响,某科学家将一片土地划分成200个![]() 的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
表1:施用新化肥小麦产量频数分布表
| 小麦产量 |
|
|
|
|
|
| 频数 | 10 | 35 | 40 | 10 | 5 |
表2:不施用新化肥小麦产量频数分布表
| 小麦产量 |
|
|
|
|
| 频数 | 15 | 50 | 30 | 5 |
(1)完成下面频率分布直方图;


施用新化肥后小麦产量的频率分布直方图 不施用新化肥后小麦产量的频率分布直方图
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计施用化肥和不施用化肥的一小块土地的小麦平均产量;
(3)完成下面2×2列联表,并回答能否有99.5%的把握认为“施用新化肥和不施用新化肥的小麦产量有差异”
表3:
| 小麦产量小于20kg | 小麦产量不小于20kg | 合计 | |
| 施用新化肥 |
|
| |
| 不施用新化肥 |
|
| |
| 合计 |
|
附:![]()
|
| 0.050 0.010 0.005 0.001 |
|
| 3.841 6.635 7.879 10.828 |
查看答案和解析>>
科目: 来源: 题型:
已知七位评委为某民族舞蹈参赛演员评定分数的茎叶图如右,图中左边为十位数,右边为个位数.去掉一个最高分和一个最低分,所剩数据的平均数和方差分别为 ( )
A.84, 4.84 B.84, 1.6
C.85, 1.6 D.85, 4
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com