
科目: 来源: 题型:
(本题满分11分)张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为![]() ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为![]() ,
,![]() .
.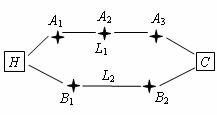
(Ⅰ)若走L1路线,求最多遇到1次红灯的概率;
(Ⅱ)若走L2路线,求遇到红灯次数![]() 的数学期望;
的数学期望;
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助张先生从上述两条路线中选择一条最好的上班路线,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
甲、乙两人各进行3次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率为
,乙每次击中目标的概率为![]() ,(1)记甲击中目标的次数为
,(1)记甲击中目标的次数为![]() ,求
,求![]() 的概率分布及数学期望
的概率分布及数学期望![]() ;
;
(2)求乙至多击中目标2次的概率; (3)求甲恰好比乙多击中目标2次的概率.
查看答案和解析>>
科目: 来源: 题型:
(本题满分12分)某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
( I ) 求这次铅球测试成绩合格的人数;
 (II) 用此次测试结果估计全市毕业生的情况.若从今年的高中毕业生中随机抽取两名,记
(II) 用此次测试结果估计全市毕业生的情况.若从今年的高中毕业生中随机抽取两名,记![]() 表示两人中成绩不合格的人数,求
表示两人中成绩不合格的人数,求![]() 的数学期望和方差.
的数学期望和方差.
查看答案和解析>>
科目: 来源: 题型:
(本题满分12分)
为了防止受到核污染的产品影响我国民众的身体健康,某地要求产品在进入市场前必须进行两轮核辐射检测,
只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为![]() ,第二轮检测不合
,第二轮检测不合
格的概率为![]() ,每轮检测结果只有“合格”、“不合格”两种,且两轮检测是否合格相互没有影响.
,每轮检测结果只有“合格”、“不合格”两种,且两轮检测是否合格相互没有影响.
(Ⅰ)求该产品不能销售的概率;
(Ⅱ)如果产品可以销售,则每件产品可获利40元;如果产品不能销售,则每件产品亏损80元(即获利![]()
元).已知一箱中有产品4件,记一箱产品获利X元,求EX.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)对某班级50名同学一年来参加社会实践的次数进行的调查统计,得到如下频率分布表:
| 参加次数 | 0 | 1 | 2 | 3 |
| 人数 | 0.1 | 0.2 | 0.4 | 0.3 |
根据上表信息解答以下问题:
(Ⅰ)从该班级任选两名同学,用η表示这两人参加社会实践次数之和,记“函数![]() 在区间
在区间![]() ,
,![]() 内有零点”的事件为
内有零点”的事件为![]() ,求
,求![]() 发生的概率
发生的概率![]() ;
;
(Ⅱ)从该班级任选两名同学,用ξ表示这两人参加社会实践次数之差的绝对值,求随机变量ξ的分布列及数学期望Eξ.
查看答案和解析>>
科目: 来源: 题型:
马老师从课本上抄录一个随机变量![]() 的概率分布律如下表:
的概率分布律如下表:
|
| 1 | 2 | 3 |
|
| ? | ! | ? |
请小牛同学计算![]() 的数学期望.尽管“!”处完全无法看清,且两个“?”处字迹模糊,但能断定这两个“?”处的数值相同.据此,小牛给出了正确答案
的数学期望.尽管“!”处完全无法看清,且两个“?”处字迹模糊,但能断定这两个“?”处的数值相同.据此,小牛给出了正确答案![]() = .
= .
查看答案和解析>>
科目: 来源: 题型:
(本小题满分13分) 如图,![]() 两点之间有
两点之间有![]() 条网线并联,它们能通过的最大信息量分别为
条网线并联,它们能通过的最大信息量分别为![]() 现从中任取三条网线且使每条网线通过最大的信息量
现从中任取三条网线且使每条网线通过最大的信息量
|
(II)求选取的三条网线可通过信息总量的数学期望
查看答案和解析>>
科目: 来源: 题型:
(本小题满分14分)在一次抗洪抢险中,准备用射击的方法引爆从河上游漂流而下的一只巨大汽油罐。已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功.每次射击命中的概率都是![]() ,每次命中与否互相独立。
,每次命中与否互相独立。
(I)求恰好射击5次引爆油罐的概率;
(II)如果引爆或子弹打光则停止射击,设射击次数为![]() ,求
,求![]() 的分布列及
的分布列及![]() 的数学期望。
的数学期望。
查看答案和解析>>
科目: 来源: 题型:
某运动员投篮命中率为![]() ,他重复投篮5次,若他命中一次得10分,没命中不得分,命中次数为
,他重复投篮5次,若他命中一次得10分,没命中不得分,命中次数为![]() ,得分为
,得分为![]() ,则
,则![]() 分别为( *** )
分别为( *** )
A.![]() ,60 B.3,12 C.3,120 D.3,
,60 B.3,12 C.3,120 D.3, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com