某射手射击所得环数的分布列如下：

已知的期望E=8.9，则y的值为             。

有甲、乙两个箱子，甲箱内有6张卡片，其中有1张写有数字0，3张写有1，2张写有2，乙箱内有3张卡片，其中有1张写有1，2张写有2，现从甲箱中取2张卡片，乙箱中取1张卡片，共取了3张卡片.

(1)求取出的3张卡片上都写有数字1的概率;

(2)设取出的3张卡片上的数字之积为.

①求的概率;           ②求的数学期望.

某生物兴趣小组对A、B两种植物种子的发芽率进行验证性实验,每实验一次均种下一粒A种子和一粒B种子.已知A、B两种种子在一定条件下每粒发芽的概率分别为.假设两种种子是否发芽互相不受影响,任何两粒种子是否发芽互相也没有影响。

（1）求3粒A种子，至少有一粒未发芽的概率；

（2）求A、B各3粒种子，A至少2粒发芽且B全发芽的概率；

（3）假设对B种子的实验有2次发芽，则终止实验，否则继续进行，但实验的次数最多不超过5次，求对B种子的发芽实验终止时，实验次数的概率分布和数学期望.

（本小题13分）

（A卷）在1，2，3，4，5的所有排列中，

（1）求满足的概率；

（2）记为某一排列中满足的个数，求的分布列和数学期望．

(本小题满分12分)袋中装着标有数字1，2，3，4，5的小球各2个，从袋中任取3个小球，按3个小球上最大数字的9倍计分，每个小球被取出的可能性都相等，用ξ表示取出的3个小球上的最大数字，

求：（1）取出的3个小球上的数字互不相同的概率；    

(2)随机变量ξ的概率分布和数学期望；

(3)计分介于20分到40分之间的概率.

某次月考数学第Ⅰ卷共有8道选择题，每道选择题有4个选项，其中只有一个是正

确的；评分标准为：“每题只有一个选项是正确的，选对得5分，不选或选错得0分．”某考生每道题都给出一个答案，已确定有5道题的答案是正确的，而其余3道题中，有一道题可判断出两个选项是错误的，有一道题可以判断出一个选项是错误的，还有一道题因不了解题意而乱猜，试求该考生：

 （Ⅰ）得40分的概率；

（Ⅱ）得多少分的可能性最大？

（Ⅲ）所得分数的数学期望．

(本小题满分12分)

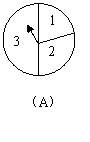
如图所示,有两个独立的转盘、.两个图中三个扇形区域的圆心角分别为为、、.用这两个转盘玩游戏，规则如下：依次随机转动两个转盘再随机停下（指针固定不会动,当指针恰好落在分界线时,则这次结果无效,重新开始），记转盘指针对的数为，转盘指针对的数为.记的值为,每转动一次则得到奖励分分.

（１）求<2且>1的概率；

（２）求某人玩一次这种游戏可得奖励分的期望值；

（３）某人玩12次，求他平均可以得到多少奖励分？

（本题满分12分）

 某篮球联赛的总决赛在甲、乙两队之间角逐。采用七场四胜制，即有一队胜四场，则此队获胜，同时比赛结束。在每场比赛中，两队获胜的概率相等。根据以往资料统计，每场比赛组织者可获门票收入32万元，两队决出胜负后，问：

(1)组织者在此次决赛中，获门票收入为128万元的概率是多少？

(2)设组织者在此次决赛中获门票收入为，求的分布列及。

某计算机网络有个终端，每个终端在一天中使用的概率都是，则这个网络在一天中平均使用的终端个数为（    ）

A.      B.     C.         D. 

哈尔滨市第六中学为绿化环境，移栽甲乙两种大树各株，已知甲树种每株成活率为，乙树种每株成活率为，各株大树是否成活互不影响。求

（1）两种大树各成活一株的概率；

(2)设两种大树共成活的株数为，求的分布列和期望；

(3)设表示“甲乙两种大树成活株数之和等于”这一事件，用表示“甲成活的株数大于乙成活的株数”这一事件，求。