
科目: 来源: 题型:
(本小题满分13分)(Ⅰ)小问5分,(Ⅱ)小问8分)
某市公租房的房源位于A,B,C三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的求该市的任4位申请人中:
(Ⅰ)恰有2人申请A片区房源的概率;
(Ⅱ)申请的房源所在片区的个数![]() 的分布列与期望
的分布列与期望
查看答案和解析>>
科目: 来源: 题型:
某毕业生参加人才招聘会,分别向甲、乙、丙三个公司投递了个人简历,假定该毕业生得到甲公司面试的概率为![]() ,得到乙丙公司面试的概率为
,得到乙丙公司面试的概率为![]() ,且三个公司是否让其面试是相互独立的。记X为该毕业生得到面试得公司个数。若
,且三个公司是否让其面试是相互独立的。记X为该毕业生得到面试得公司个数。若![]() ,则随机变量X的数学期望
,则随机变量X的数学期望
![]()
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种家和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
(I)假设n=4,在第一大块地中,种植品种甲的小块地的数目记为X,求X的分布列和数学期望;
(II)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如下表:
| 品种甲 | 403 | 397 | 390 | 404 | 388 | 400 | 412 | 406 |
| 品种乙 | 419 | 403 | 412 | 418 | 408 | 423 | 400 | 413 |
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
附:样本数据![]() 的的样本方差
的的样本方差![]() ,其中
,其中![]() 为样本平均数.
为样本平均数.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
某饮料公司招聘了一名员工,现对其进行一项测试,以使确定工资级别,公司准备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为A饮料,另外4杯为B饮料,公司要求此员工一一品尝后,从8杯饮料中选出4杯A饮料,若4杯都选对,则月工资定为3500元,若4杯选对3杯,则月工资定为2800元,否则月工资定为2100元,令X表示此人选对A饮料的杯数,假设此人对A和B两种饮料没有鉴别能力.
(1)求X的分布列;
(2)求此员工月工资的期望。
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
某商店试销某种商品20天,获得如下数据:
| 日销售量(件) | 0 | 1 | 2 | 3 |
| 频数 | 1 | 5 | 9 | 5 |
试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充至3件,否则不进货,将频率视为概率。
(Ⅰ)求当天商品不进货的概率;
(Ⅱ)记X为第二天开始营业时该商品的件数,求X的分布列和数学期型。
查看答案和解析>>
科目: 来源: 题型:
(本小题满分13分)
为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽出取14件和5件,测量产品中的微量元素x,y的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
(1)已知甲厂生产的产品共有98件,求乙厂生产的产品数量;
(2)当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品。用上述样本数据估计乙厂生产的优等品的数量;
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数![]() 的分布列极其均值(即数学期望)。
的分布列极其均值(即数学期望)。
查看答案和解析>>
科目: 来源: 题型:
本小题共13分
以下茎叶图记录了甲、乙两组个四名同学的植树棵树。乙组记录中有一个数据模糊,无法确认,在图中以X表示。

(Ⅰ)如果X=8,求乙组同学植树棵树的平均数和方差;
(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵树Y的分布列和数学期望。
(注:方差![]() ,其中
,其中![]() 为
为![]() ,
,![]() ,……
,…… ![]() 的平均数)
的平均数)
查看答案和解析>>
科目: 来源: 题型:
(本小题满分13分)
工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人。现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别![]() ,假设
,假设![]() 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.
(Ⅰ)如果按甲最先,乙次之,丙最后的顺序派人,求任务能被完成的概率。若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(Ⅱ)若按某指定顺序派人,这三个人各自能完成任务的概率依次为![]() ,其中
,其中![]() 是
是![]() 的一个排列,求所需派出人员数目
的一个排列,求所需派出人员数目![]() 的分布列和均值(数字期望)
的分布列和均值(数字期望)![]() ;
;
(Ⅲ)假定![]() ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小。
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小。
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛,甲对A,乙对B,丙对C各一盘,已知甲胜A,乙胜B,丙胜C的概率分别为0.6,0.5,0.5,假设各盘比赛结果相互独立。
(Ⅰ)求红队至少两名队员获胜的概率;
(Ⅱ)用![]() 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分13分)
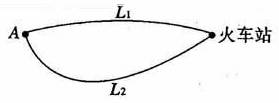
如图,A地到火车站共有两条路径L1和L2,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:
| 时间(分钟) | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 |
| L1的频率 | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 |
| L2的频率 | 0 | 0.1 | 0.4 | 0.4 | 0.1 |
现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站。
(Ⅰ)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
 (Ⅱ)用X表示甲、乙两人中在允许的时间内能赶到火车站的人数,针对(Ⅰ)的选择方案,求X的分布列和数学期望。
(Ⅱ)用X表示甲、乙两人中在允许的时间内能赶到火车站的人数,针对(Ⅰ)的选择方案,求X的分布列和数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com