（本小题14分）甲和乙参加有奖竞猜闯关活动，活动规则：①闯关过程中，若闯关成功则继续答题；若没通关则被淘汰；②每人最多闯3关；③闯第一关得10万奖金，闯第二关得20万奖金，闯第三关得30万奖金，一关都没过则没有奖金。已知甲每次闯关成功的概率为，乙每次闯关成功的概率为。
　　（1）设乙的奖金为，求的分布列和数学期望；
　　（2）求甲恰好比乙多30万元奖金的概率.

（本小题满分12分）

现有一游戏装置如图，小球从最上方入口处投入，每次遇到黑色障碍物，等可能地向左，右两边落下。

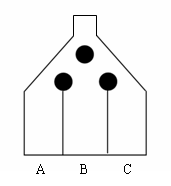游戏规则为：若小球最终落入A槽，得10张奖票；若落入B槽，得5张奖票；若落入C槽，得重投一次的机会，但投球的总次数不超过3次。

求投球一次，小球落入B槽的概率；

设玩一次游戏能获得的奖票数为随机变量 ，求的分布列及数学期望。

（本小题满分12分）某公司对工厂A的一批产品进行了抽样检测。右图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100),[100，102)，[102，104),[10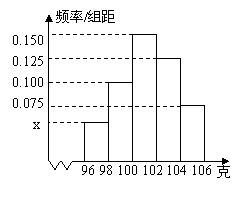4，106]。

（1）求图中x的值；

（2）若将频率视为概率，从这批产品中有放回地随机抽取3件，求至多有2件产品的净重在的概率；

（3）经过考察后，该公司决定在2011年年初投资到工厂A50万元，到年底可能获利，也可能亏损，且这两种情况发生的概率分别为合格产品和不合格产品的概率（若产品净重在为合格产品，其余为不合格产品）。设2011年底公司的投资总资产（本金+利润）为，求的分布列及数学期望。

（本小题满分12分）

如图是在竖直平面内的一个“通道游戏”．图中竖直线段和斜线段都表示通道，并且在交点处相遇，若竖直线段有第一条的为第一层，有二条的为第二层，……，依次类推．现有一颗小弹子从第一层的通道里向下运动．记小弹子落入第层第个竖直通道（从左至右）的概率为．（已知在通道的分叉处，小弹子以相同的概率落入每个通道）

（Ⅰ）求的值，并猜想的表达式．（不必证明）

（Ⅱ）设小弹子落入第6层第个竖直通道得到分数为，

其中，试求的分布列及数学期望．

（本小题满分12分）

已知函数，，，，，

，将它们分别写在六张卡片上，放在一个盒子中，

（Ⅰ）现从盒子中任取两张卡片，将卡片上的函数相加得到一个新函数，求所得的函数是奇函数的概率；

（Ⅱ）从盒子中任取两张卡片，已知其中一张卡片上的函数为奇函数，求另一张卡片上的函数也是奇函数的概率；

（Ⅲ）现从盒子中逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数的卡片则停止抽取，否则继续进行，求抽取次数的分布列和数学期望．

（本小题共13分）

某商场一号电梯从1层出发后可以在2、3、4层停靠.已知该电梯在1层载有4位乘客，假设每位乘客在2、3、4层下电梯是等可能的.

(Ⅰ) 求这4位乘客中至少有一名乘客在第2层下电梯的概率；

(Ⅱ) 用表示4名乘客在第4层下电梯的人数，求的分布列和数学期望.

( 本小题满分12分)

甲、乙两位学生参加数学竞赛培训．现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次．记录如下：

甲：82 81 79 78 95 88 93 84     乙：92 95 80 75 83 80 90 85

  （I）画出甲、乙两位学生成绩的茎叶图，指出学生乙成绩的中位数；

（II）现要从中选派一人参加数学竞赛，从平均状况和方差的角度考虑，你认为派哪位学生参加合适?请说明理由；

（III）若将频率视为概率，对学生甲在今后的三次数学竞赛成绩进行预测，记这三次成绩中高于80分的次数为，求的分布列及数学期望.

（本小题满分12分）

2011年4月28日，世界园艺博览会已在西安正式开园，正式开园前，主办方安排了4次试运行，为了解前期准备情况和试运行中出现的问题，以做改进，组委会组织了一次座谈会，共邀请20名代表参加，他们分别是游客15人，志愿者5人。

（I）从这20名代表中随机选出3名谈建议，求至少有1人是志愿者的概率；

（II）若随机选出2名代表发言，表示其游客人数，求的分布列和数学期望。

（本题满分12分）

某种项目的射击比赛，开始时选手在距离目标100m处射击，若命中则记3分，且停止射击．若第一次射击未命中，可以进行第二次射击，但需在距离目标150m处，这时命中目标记2分，且停止射击．若第二次仍未命中，还可以进行第三次射击，此时需在距离目标200m处，若第三次命中则记1分，并停止射击．若三次都未命中则记0分，并停止射击．已知选手甲的命中率与目标的距离的平方成反比，他在100m处击中目标的概率为，且各次射击都相互独立．

（Ⅰ）求选手甲在三次射击中命中目标的概率；

（Ⅱ）设选手甲在比赛中的得分为，求的分布列和数学期望．