
科目: 来源: 题型:
(本小题共14分)
 张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为
张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为![]() ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为![]() ,
,![]() .
.
(Ⅰ)若走L1路线,求最多遇到1次红灯的概率;
(Ⅱ)若走L2路线,求遇到红灯次数![]() 的数学期望;
的数学期望;
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助张先生从上述两条路线中选择一条最好的上班路线,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
某电视台拟举行“团队共享”冲关比赛,其规则如下:比赛共设有“常识关”和“创新关”两关,每个团队共两人,每人各冲一关,“常识关”中有2道不同必答题,“创新关”中有3道不同必答题;如果“常识关”中的2道题都答对,则冲“常识关”成功且该团队获得单项奖励900元,否则无奖励;如果“创新关”中的3道题至少有2道题答对,则冲“创新关”成功且该团队获得单项奖励1800元,否则无奖励.现某团队中甲冲击“常识关”,乙冲击“创新关”,已知甲回答“常识关”中每道题正确的概率都为![]() ,乙回答“创新关”中每道题正确的概率都为
,乙回答“创新关”中每道题正确的概率都为![]() ,且两关之间互不影响,每道题回答正确与否相互独立.
,且两关之间互不影响,每道题回答正确与否相互独立.
(I)求此冲关团队在这5道必答题中只有2道回答正确且没有获得任何奖励的概率;
(Ⅱ)记此冲关团队获得的奖励总金额为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
济南市开展支教活动,有五名教师被随机的分到A、B、C三个不同的乡镇中学,且每个乡镇中学至少一名教师,
(1)求甲乙两名教师同时分到一个中学的概率;
(2)求A中学分到两名教师的概率;
(3)设随机变量X为这五名教师分到A中学的人数,求X的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:
本小题满分12分)
某公司在产品上市前需对产品做检验,公司将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(I )若公司库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验.求至少有1件是合格品的概率;k&s%5¥u
( II)若该公司发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才收这批产品,否则拒收.求该商家可能检验出不合格产品数![]() 的分布列及期望
的分布列及期望![]() ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图5所示,成绩不小于90分为及格.
| 甲 | 乙 | |
| 257 368 58 68 | 7 8 9 10 | 89 678 1235 1 |
(Ⅰ)甲班10名同学成绩的标准差 乙班10名同学成绩的标准差(填“>”,“<”);
(Ⅱ)从两班10名同学中各抽取一人,已知有人及格,求乙班同学不及格的概率;
(Ⅲ)从甲班10人中取一人,乙班10人中取两人,三人中及格人数记为X,
|
查看答案和解析>>
科目: 来源: 题型:
一种抛硬币游戏的规则是:抛掷一枚硬币,每次正面向上得1分,反面向上得2分.
(1)设抛掷5次的得分为![]() ,求
,求![]() 的分布列和数学期望E
的分布列和数学期望E![]() ;
;
(2)求恰好得到n![]() 分的概率.
分的概率.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行 ,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):
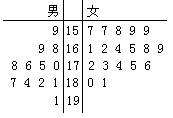 若身高在175cm以上(包括175cm)定义为“高个子”,
若身高在175cm以上(包括175cm)定义为“高个子”,
身高在175cm以下(不包括175cm)定义为“非高个子”,
且只有“女高个子”才担任“礼仪小姐”。
(1)如果用分层抽样的方法从“高个子”和“非高个子”中
中提取5人,再从这5人中选2人,那么至少有一人是
“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用![]() 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望。
的数学期望。
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有![]() 次选题答题的机会,选手累计答对
次选题答题的机会,选手累计答对![]() 题或答错
题或答错![]() 题即终止其初赛的比赛:答对
题即终止其初赛的比赛:答对![]() 题者直接进入决赛,答错
题者直接进入决赛,答错![]() 题者则被淘汰.已知选手甲答对每个问题的概率相同,并且相互之间没有影响,答题连续两次答错的概率为
题者则被淘汰.已知选手甲答对每个问题的概率相同,并且相互之间没有影响,答题连续两次答错的概率为![]() .
.
⑴求选手甲可进入决赛的概率;
⑵设选手甲在初赛中答题的个数为![]() ,试求
,试求![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
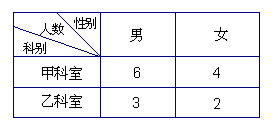
某单位甲乙两个科室人数及男女工作人员分布情况见右表.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两个科室中共抽取3名工作人员进行一项关于“低碳生活”的调查.
(1)求从甲、乙两科室各抽取的人数;
(2)求从甲科室抽取的工作人员中至少有1名女性的概率;
(3)记![]() 表示抽取的3名工作人员中男性的人数,求
表示抽取的3名工作人员中男性的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
现有三枚外观一致的硬币,其中两枚是均匀硬币另一枚是不均匀的硬币,这枚不均匀的硬币抛出后正面出现的概率为![]() .现投掷这三枚硬币各1次,设
.现投掷这三枚硬币各1次,设![]() 为得到的正面个数,则随机变量
为得到的正面个数,则随机变量![]() 的数学期望
的数学期望![]() = ▲ .
= ▲ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com