（本小题满分10分）

一个口袋装有5个红球，3个白球，这些球除颜色外完全相同，某人一次从中摸出3个球，其中白球的个数为.

⑴求摸出的三个球中既有红球又有白球的概率；

⑵求的分布列及的数学期望.

（本小题满分10分）

有一种闯三关游戏规则规定如下：用抛掷正四面体型骰子（各面上分别有1，2，3，4点数的质地均匀的正四面体）决定是否过关，在闯第关时，需要抛掷次骰子，当次骰子面朝下的点数之和大于时,则算闯此关成功,并且继续闯关，否则停止闯关. 每次抛掷骰子相互独立.

   （Ⅰ）求仅闯过第一关的概率；

   （Ⅱ）记成功闯过的关数为，求的分布列和期望．

【必做题】本题满分10分．解答时应写出文字说明、证明过程或演算步骤。

某车站每天上午发出两班客车，第一班客车在8∶00，8∶20，8∶40这三个时刻随机发出，且在8∶00发出的概率为，8∶20发出的概率为，8∶40发出的概率为；第二班客车在9∶00，9∶20，9∶40这三个时刻随机发出，且在9∶00发出的概率为，9∶20发出的概率为，9∶40发出的概率为．两班客车发出时刻是相互独立的，一位旅客预计8∶10到站．求：

   （1）请预测旅客乘到第一班客车的概率；

   （2）旅客候车时间的分布列；

   （3）旅客候车时间的数学期望．

（本小题满分12分）

已知集合，集合

，集合

   （1）求从集合中任取一个元素是（3，5）的概率；

   （2）从集合中任取一个元素，求的概率；

   （3）设为随机变量，，写出的分布列，并求。

（本小题满分12分）第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行 ，为了搞好接待工作，组委会在某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图（单位：cm）：

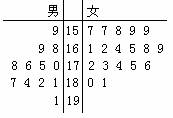        若身高在175cm以上（包括175cm）定义为“高个子”，

   身高在175cm以下（不包括175cm）定义为“非高个子”，

且只有“女高个子”才担任“礼仪小姐”。

（1）如果用分层抽样的方法从“高个子”和“非高个子”中

    中提取5人，再从这5人中选2人，那么至少有一人是

   “高个子”的概率是多少？

（2）若从所有“高个子”中选3名志愿者，用表示所选志愿者中能担任“礼仪小姐”的人数，试写出的分布列，并求的数学期望。

（本小题满分12分）某校举行环保知识大奖赛，比赛分初赛和决赛两部分，初赛采用选手选一题答一题的方式进行，每位选手最多有次选题答题的机会，选手累计答对题或答错题即终止其初赛的比赛：答对题者直接进入决赛，答错题者则被淘汰．已知选手甲答对每个问题的概率相同，并且相互之间没有影响，答题连续两次答错的概率为．

⑴求选手甲可进入决赛的概率；

⑵设选手甲在初赛中答题的个数为，试求的分布列，并求的数学期望．

（本小题满分12分）甲、乙两同学参加数学竞赛培训，现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次，具体成绩如下茎叶图所示，已知两同学这8次成绩的平均分都是85分．

⑴求；并由图中数据直观判断，甲、乙两同学中哪一位的成绩比较稳定？

⑵若将频率视为概率，对甲同学在今后3次数学竞赛成绩进行预测，记这3次成绩中高于80分的次数为，求的分布列及数学期望．

（本题满分14分）

某班同学利用国庆节进行社会实践，对岁的人群随机抽取人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：

（Ⅰ）补全频率分布直方图并求、、的值；

（Ⅱ）从岁年龄段的“低碳族”中采用分层抽样法抽取人参加户外低碳体验活动，其中选取人作为领队，记选取的名领队中年龄在岁的人数为，求的分布列和期望.

（本小题满分12分）

某班将要举行篮球投篮比赛，比赛规则是：每位选手可以选择在A区投篮2次或选择在B区投篮3次.在A区每进一球得2分，不进球得0分；在B区每进一球得3分，不进球得0分，得分高的选手胜出.已知参赛选手甲在A区和B区每次投篮进球的概率分别为和

（Ⅰ）如果选手甲以在A、B区投篮得分的期望高者为选择投篮区的标准，问选手甲应该选择哪个区投篮？

（Ⅱ）求选手甲在A区投篮得分高于在B区投篮得分的概率.

（10分）某校举行环保知识大奖赛，比赛分初赛和决赛两部分，初赛采用选手选一题答一题的方式进行，每位选手最多有次选题答题的机会，选手累计答对题或答错题即终止其初赛的比赛：答对题者直接进入决赛，答错题者则被淘汰．已知选手甲答对每个问题的概率相同，并且相互之间没有影响，答题连续两次答错的概率为．

⑴求选手甲可进入决赛的概率；

⑵设选手甲在初赛中答题的个数为，试求的分布列，并求的数学期望．