若＜＜ 0 ，则下列结论正确的是（　    ）

 A、>b²     B、 b>b²     C、  ＞2     D、

（本小题满分10分）设集合，．

（Ⅰ）求集合；      

（Ⅱ）若不等式的解集为，求，的等差中项．

已知函数，，若对任意实数，与的值至少有一个为正数，则实数的取值范围是__________．        

（本小题满分12分）

阅读下面内容，思考后做两道小题。

在一节数学课上，老师给出一道题，让同学们先解，题目是这样的：

已知函数f(x)=kx+b，1≤f(1)≤3，－1≤f(－1)≤1，求Z=f(2)的取值范围。

题目给出后，同学们马上投入紧张的解答中，结果很快出来了，大家解出的结果有很多个，下面是其中甲、乙两个同学的解法：

甲同学的解法：由f(1)=k+b，f(－1)=－k+b得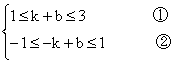

①+②得：0≤2b≤4，即0≤b≤2               ③

② ×(－1)+①得：－1≤k－b≤1             ④

④+②得：0≤2k≤4                                               ⑤

③+⑤得：0≤2k+b≤6。

又∵f(2)=2k+b

∴0≤f(2)≤6，0≤Z≤6

      乙同学的解法是：由f(1)=k+b，f(－1)=－k+b得

①+②得：0≤2b≤4，即：0≤b≤2                        ③

①－②得：2≤2k≤2，即：1≤k≤1

∴k=1，

∵f(2)=2k+b=1+b

由③得：1≤f(2)≤3

∴：1≤Z≤3

（Ⅰ）如果课堂上老师让你对甲、乙两同学的解法给以评价，你如何评价？

（Ⅱ）请你利用线性规划方面的知识，再写出一种解法。

若，则能成立的不等式是

A.            B.           C.            D.

已知  （），给出下列不等式：①，②，

③，④，⑤，其中一定成立的是                。

（填上你认为一定成立的所有序号）

如图，两个工厂A、B相距3(Km)，现要在以AB为直径的圆弧上的某一点处建一幢办公楼（异于A、B点）.据测算此办公楼受工厂A的“噪音影响度”与距离AP的平方成反比，比例系数是1；办公楼受工厂B的“噪音影响度” 与距离BP的平方也成反比，比例系数是4。办公楼受A、B两厂的“总噪音影响度”y是为受A、B两厂“噪音影响度”之和，设AP为x(Km).

（1）求“总噪音影响度” y关于x的函数关系式，并指出函数的定义域；

（2）当AP为多少时，“总噪音影响度”最小.

设x，y满足约束条件。若目标函数（，）的最大值为12，则的最小值为

       （A）       （B）  （C）       （D）4

现有一批货物用轮船甲地运往乙地距离为500海里，已知该船最大速度为45海里/小时，每小时运输成本由燃料费用和其他费用组成。轮船每小时的燃料费用与轮船速度的平方成正比，其余费用为每小时960元。已知轮船速度为20海里/小时的全程运输成本为30000元。

（1）把全程运输成本y（元）表示为速度x(海里/小时)的函数；

（2）为了使全程运输成本最小，轮船应为多大速度行驶？

（14分）

已知函数（），且方程有两个实数根为；

（1）求函数的解析式。

（2）当时，若恒成立，求的取值范围。

（3）设，解关于的不等式：