
科目: 来源: 题型:
(必做题)(本小题满分10分)
电视台举办猜奖活动,参与者需先后回答两道选择题:问题A有四个选项,问题B有六个选
项,但都只有一个选项是正确的。正确回答问题A可获奖金m元,正确回答问题B可获奖金n元。
活动规定:①参与者可任意选择回答问题的顺序;②如果第一个问题回答错误,则该参与者猜奖活动中止。
查看答案和解析>>
科目: 来源: 题型:
(本题满分10分)
 有一种舞台灯,外形是正六棱柱,在其每一个侧面(编号为①②③④⑤⑥)上安装5只颜色各异的灯,假若每只灯正常发光的概率为
有一种舞台灯,外形是正六棱柱,在其每一个侧面(编号为①②③④⑤⑥)上安装5只颜色各异的灯,假若每只灯正常发光的概率为![]() , 若一个侧面上至少有3只灯发光,则不需要更换这个面,否则需要更换这个面,假定更换一个面需要100元,用ξ表示更换费用.
, 若一个侧面上至少有3只灯发光,则不需要更换这个面,否则需要更换这个面,假定更换一个面需要100元,用ξ表示更换费用.
(1)求①号面需要更换的概率;
(2)求6个面中恰好有2个面需要更换的概率;
(3)写出ξ的分布列,并求ξ的数学期望.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是p,电流能通过T4的概率是0.9.电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999.
(Ⅰ)求p;
(Ⅱ)求电流能在M与N之间通过的概率;
(Ⅲ)![]() 表示T1,T2,T3,T4中能通过电流的元件个数,求
表示T1,T2,T3,T4中能通过电流的元件个数,求![]() 的期望.
的期望.

查看答案和解析>>
科目: 来源: 题型:
(本小题满分10分)
某工厂生产甲、乙两种产品,甲产品的一等品率为80%,二等品率为20%;乙产品的一等品率为90%,二等品率为10%。生产1件甲产品,若是一等品则获得利润4万元,若是二等品则亏损1万元;生产1件乙产品,若是一等品则获得利润6万元,若是二等品则亏损2万元。设生产各种产品相互独立。
记X(单位:万元)为生产1件甲产品和1件乙产品可获得的总利润,求X的分布列;
求生产4件甲产品所获得的利润不少于10万元的概率。
查看答案和解析>>
科目: 来源: 题型:
(本小题满分高☆考♂资♀源*网12分)
某迷宫有三个通道,进入迷宫的每个人都要经过一扇智能门。首次到达此门,系统会随机(即等可能)为你打开一个通道,若是1号通道,则需要1小时走出迷宫;若是2号、3号通道,则分别需要2小时、3小时返回智能门。再次到达智能门时,系统会随机打开一个你未到过的通道,直至走完迷宫为止。令![]() 表示走出迷宫所需的时间。
表示走出迷宫所需的时间。
求![]() 的分布列;
的分布列;
求![]() 的数学期望。
的数学期望。
查看答案和解析>>
科目: 来源: 题型:
(本小题满分13分)
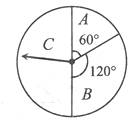
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(I)若某位顾客消费128元,求返券金额不低于30元的概率;
(II)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为X(元).
 求随机变量X的分布列和数学期望。
求随机变量X的分布列和数学期望。
查看答案和解析>>
科目: 来源: 题型:
(本小题共13分)
某校高三年级有男生105人,女生126人,教师42人,用分层抽样的方法从中抽取13人,进行问卷调查.设其中某项问题的选择支为“同意”,“不同意”两种,且每人都做了一种选择.下面表格中提供了被调查人答卷情况的部分信息.
| 同意 | 不同意 | 合计 | |
| 教师 | 1 | ||
| 女生 | 4 | ||
| 男生 | 2 |
(I)请完成此统计表;
(II)试估计高三年级学生“同意”的人数;
(III)从被调查的女生中选取2人进行访谈,求选到的两名学生中,恰有一人“同意”一人“不同决的概率.”
查看答案和解析>>
科目: 来源: 题型:
(14分)
某工厂师徒二人各加工相同型号的零件2个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为![]() ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为![]()
(I)求徒弟加工2个零件都是精品的概率;
(II)求徒弟加工该零件的精品数多于师父的概率;
(III)设师徒二人加工出的4个零件中精品个数为![]() ,求
,求![]() 的分布列与均值E
的分布列与均值E![]() .
.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分13分)
在一次数学统考后,某班随机抽取10名同学的成绩进行样本分析,获得成绩数据的茎叶图如下.
(Ⅰ)计算样本的平均成绩及方差;
(Ⅱ)现从10个样本中随机抽出2名学生的成绩,设选出学生的分数为90分以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和均值.
的分布列和均值.
| 9 | 2 | 8 | 8 |
| 8 | 5 | 5 | |
| 7 | 4 | 4 | 4 |
| 6 | 0 | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com