
科目: 来源: 题型:
|
(Ⅰ)求证:直线BC1//平面AB1D;
(Ⅱ)求二面角B1—AD—B的大小;
(Ⅲ)求三棱锥C1—ABB1的体积.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
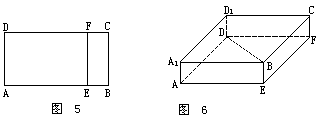
有一矩形纸片ABCD,AB=5,BC=2,E,F分别是AB,CD上的点,且BE=CF=1,把纸片沿EF折成直二面角.
(1)求BD的距离;
(2)求证AC,BD交于一点且被这点平分.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,
∠ADB=60°,E、F分别是AC、AD上的动点,且![]()
|
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD?
查看答案和解析>>
科目: 来源: 题型:
|
(Ⅰ)求证:A′F⊥C′E;
(Ⅱ)求二面角B′—EF—B的大小.
查看答案和解析>>
科目: 来源: 题型:
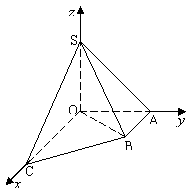 (本题满分16分)如图直角梯形OABC中,∠COA=∠OAB=
(本题满分16分)如图直角梯形OABC中,∠COA=∠OAB=![]() ,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
⑴求![]() 的大小(用反三角函数表示);
的大小(用反三角函数表示);
⑵设![]()
①![]() ②OA与平面SBC的夹角
②OA与平面SBC的夹角![]() (用反三角函数表示);
(用反三角函数表示);
③O到平面SBC的距离.
⑶设![]()
①![]() . ②异面直线SC、OB的距离为 .(注:⑶只要求写出答案)
. ②异面直线SC、OB的距离为 .(注:⑶只要求写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com