将杨辉三角（如图（1））中的每一个数都换成分数，就得到一个如图（2）所示的分数三角形，称为莱布尼茨三角形．从莱布尼茨三角形可以看出：                            

，其中    ▲     ．w w w.k s 5u.c o m

若，则二项式展开式中项的系数为     ___.

已知等式，

其中a_i（i=0，1，2，…，10）为实常数．

求：(1) （2）的值；

（本题满分14分）

已知集合A，B满足，试分别用分类计数原理、分步计数原理求出A，B的组数.

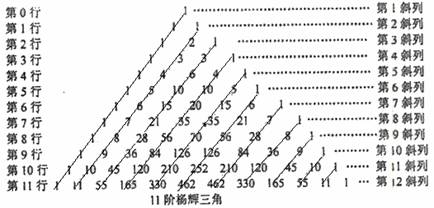
（本题满分15分）杨辉是中国南宋末年的一位杰出的数学家、数学教育家，杨辉三角是杨辉的一大重要研究成果，它的许多性质与组合数的性质有关，杨辉三角中蕴藏了许多优美的规律．下图是一个11阶杨辉三角：

（1）求第20行中从左到右的第3个数；

   （2）若第行中从左到右第13与第14个数的比为，求的值；

   （3）写出第行所有数的和，写出阶（包括阶）杨辉三角中的所有数的和；

（4）在第3斜列中，前5个数依次为1，3，6，10，15；第4斜列中，第5个数为35，我们发现，事实上，一般地有这样的结论：第斜列中（从右上到左下）前个数之和，一定等于第斜列中第个数．

        试用含有，的数学式子表示上述结论，并证明．

（本小题满分16分）

已知数列的首项为，  .

（1）若为常数列，求的值；

（2）若为公比为的等比数列，求的解析式；

（3）数列能否成等差数列，使得对一切都成立.若能，求出数列的通项公式；若不能，试说明理由.

如图，把数列中的所有项按照从小到大，从左到右的顺序写成如图所示的数表，且第行有个数.若第行从左边起的第个数记为，则这个数可记为　▲　．

（Ⅰ）设展开式中的系数是10，求n的值；

　（Ⅱ）利用二项式定理证明：．

设，，（1）当时，求；（2）当时，展开式中的系数是20，求的值；

（3）展开式中的系数是19，当，变化时，求系数的最小值．

设函数.

（1）当时，求的展开式中二项式系数最大的项；

（2）若且，求；

（3）设是正整数，为正实数，实数满足，求证：

．