(本题满分12分)如图，现在要在一块半径为1 m，圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ，使点P在弧AB上，点Q在OA上，点M，N在OB上，设∠BOP＝θ，MNPQ的面积为S.

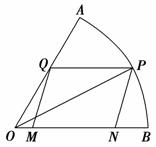(1)求S关于θ的函数关系式；

(2)求S的最大值及相应θ的值．

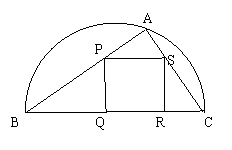如图，某园林单位准备绿化一块直径为BC的半圆形空地，的外面种草， 的内接正方形PQRS为一水池，其余的地方种花，若，设的面积为，正方形的面积为．

（1）用表示和；

（2）当固定，变化时，求取最小值时的角．

使sinα≥cosα成立的α的一个取值区间是（    ）

A.         B.          C.        D.

（12分）设y=A sin(ωx+j)(A＞0，ω＞0，|j|＜π)最高点D的坐标为（2，），由最高点运动到相邻的最低点时，曲线与轴交点E的坐标为(6，0)，(1)求A、ω、j的值；(2)求出该函数的频率，初相和单调区间．

如图，某小区准备在一直角围墙内的空地上植造“绿地”，其中，长可根据需要进行调节（足够长），现规划在内接正方形内种花，其余地方种草，设种草的面积与种花的面积的比为，

（1）设角，将表示成的函数关系；

（2）当为多长时，有最小值，最小值是多少？

（本小题满分12分）

如图所示，有块正方形的钢板ABCD，其中一个角有部分损坏,现要把它截成一块正方形的钢板EFGH. 在直角三角形GFC中，∠GFC =θ ．若截后的正方形钢板EFGH的面积是原正方形钢板ABCD的面积的三分之二，求θ的值．

（本小题满分12分）

某体育馆拟用运动场的边角地建一个矩形的健身室(如图所示)，ABCD是一块边长为50 m的正方形地皮，扇形CEF是运动场的一部分，其半径为40 m，矩形AGHM就是拟建的健身室，其中G、M分别在AB和AD上，H在   上。设矩形AGHM的面积为S，∠HCF=θ，请将S表示为θ的函数，并指出当点H在    的何处时，该健身室的面积最大，最大面积是多少？ 

（本小题满分16分）

某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其在

40分钟的一节课中，注意力指数p与听课时间t（单位：分钟）之间的关系满足如图

所示的曲线．当时，曲线是二次函数图象的一部分，当时，曲线

是函数(，)图象的一部分．根据专家研究，当注意力指数p大于80时学习效果最佳．

 （1）试求的函数关系式；

 （2）教师在什么时段内安排核心内容，能使得学生

      学习效果最佳？请说明理由．

（本小题满分16分）

某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其在

40分钟的一节课中，注意力指数p与听课时间t（单位：分钟）之间的关系满足如图

所示的曲线．当时，曲线是二次函数图象的一部分，当时，曲线

是函数(，)图象的一部分．根据专家研究，当注意力指数p大于80时学习效果最佳．

 （1）试求的函数关系式；

 （2）教师在什么时段内安排核心内容，能使得学生

      学习效果最佳？请说明理由．

(12分)如图, 现要在一块半径为1m, 圆心角为的扇形纸报AOB上剪出一个平行四边形MNPQ, 使点P在弧AB上, 点Q在OA上, 点M、N在OB上, 设∠BOP＝, 平行四边形MNPQ的面积为S.

(1)求S关于的函数关系式；

(2)求S的最大值及相应的角.