
科目: 来源: 题型:
(本小题满分14分)
已知一个四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点。
(1)求四棱锥P-ABCD的体积;
(2)是否不论点E在何位置,都有BD⊥AE?证明你的结论;
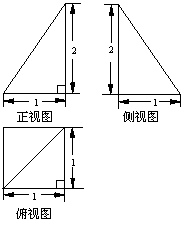 (3)若点E为PC的中点,求二面角D-AE-B的大小.
(3)若点E为PC的中点,求二面角D-AE-B的大小.
查看答案和解析>>
科目: 来源: 题型:
在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则AB2+AC2=BC2”拓展到空间,类比平面几何的勾股定理,“设三棱锥A—BCD的三个侧面ABC、ACD、ADB 两两相互垂直,则可得” ( )
A.AB2+AC2+ AD2=BC2+ CD2 + BD2 B.![]()
C.![]() D.AB2×AC2×AD2=BC2 ×CD2 ×BD2
D.AB2×AC2×AD2=BC2 ×CD2 ×BD2
查看答案和解析>>
科目: 来源: 题型:
9. 设![]() 是定义在R上的偶函数,当
是定义在R上的偶函数,当![]() 时,
时,![]() ,且
,且![]() ,则不等式
,则不等式![]() 的解集为( )
的解集为( )
A.(-1,0)∪(1,+![]() ) B.(-1,0)∪(0,1)
) B.(-1,0)∪(0,1)
C.(-![]() ,-1)∪(1,+
,-1)∪(1,+![]() ) D.(-
) D.(-![]() ,-1)∪(0,1)
,-1)∪(0,1)
查看答案和解析>>
科目: 来源: 题型:
如图,四棱锥![]() 中.
中.![]() 为矩形,
为矩形,![]() ,且
,且![]() ,
,![]() (
(![]() ),
),![]() ,
,![]() .
.![]() 为
为![]() 上一点,且
上一点,且![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
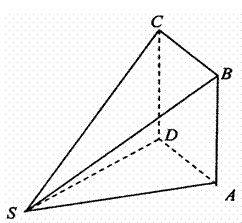 (2)
(2)![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上的点,是否存在
上的点,是否存在![]() 、
、![]() ,使
,使![]() 且
且![]() ,若存在,确定
,若存在,确定![]() 、
、![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分10分)
在极坐标系中,点![]() 坐标是
坐标是![]() ,曲线
,曲线![]() 的方程为
的方程为![]() ;以极点为坐标原点,极轴为
;以极点为坐标原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 经过点
经过点![]() 和极点.
和极点.
(1)写出直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 和曲线
和曲线![]() 相交于两点
相交于两点![]() 、
、![]() ,求线段AB的长.
,求线段AB的长.
查看答案和解析>>
科目: 来源: 题型:
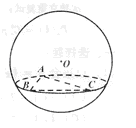
如图,在半径为3的球面上有A、B、C、三点,∠ABC=90°,BA=BC, 球心O到平
面AB C的距离是![]() ,则B、C两点的球面距离是( )
,则B、C两点的球面距离是( )
A. ![]() B. 2
B. 2![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com